搜索
【题目】已知二次函数y=ax2+bx+c的图象如图，其对称轴x=﹣1，给出下列结果： ①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a﹣b+c＜0，
则正确的结论是（ ）
A.①②③④
B.②④⑤
C.②③④
D.①④⑤
参考答案：
【答案】D
【解析】解：∵抛物线与x轴有两个交点，∴△=b2﹣4ac＞0，即b2＞4ac，故①正确； ∵抛物线对称轴为x=﹣ 
＜0，与y轴交于负半轴，∴ab＞0，c＜0，abc＜0，故②错误；
∵抛物线对称轴为x=﹣ =﹣1，∴2a﹣b=0，故③错误；
∵当x=1时，y＞0，即a+b+c＞0，故④正确；
∵当x=﹣1时，y＜0，即a﹣b+c＜0，故⑤正确；
正确的是①④⑤．
故选D．
【考点精析】利用二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案，需要熟知二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】图①，②分别是根据某地近两年6月上旬日平均气温情况绘制的折线统计图，通过观察图表回答：
去年6月上旬①
今年6月上旬②
(1)该地这两年6月上旬日平均气温分别是多少？
(2)该地这两年6月上旬日平均气温的极差分别是多少？由此可以判断哪一年6月上旬气温比较稳定？
折线图能直观地反映数据的变化趋势，能比较容易地看出变动范围，求出极差，运用时还要注意观察，通过纵横坐标的交点寻找所需要的数据信息，根据信息和题目要求作出正确分析．
观察图可知去年6月上旬的日平均气温(单位：℃)分别是：24,30,29,24,23,26,27,26,30,26.由图可知今年6月上旬的日平均气温(单位 ℃)分别是：24,26,25,26,24,26,27,26,27,26.然后求这两年的平均气温及极差．
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学活动﹣旋转变换
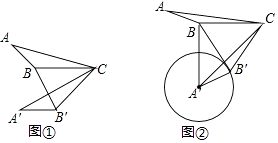
（1）如图①，在△ABC中，∠ABC=130°，将△ABC绕点C逆时针旋转50°，得到△A′B′C，连接BB′，求∠A′B′B的大小；
（2）如图②，在△ABC中，∠ABC=150°，AB=3，BC=5，将△ABC绕点C逆时针旋转60°得到△A′B′C，连接BB′，以A′为圆心，A′B′长为半径作圆． （Ⅰ）猜想：直线BB′与⊙A′的位置关系，并证明你的结论；
（Ⅱ）连接A′B，求线段A′B的长度． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=x2+bx+c与x轴交A（﹣1，0）B（3，0）两点，直线l与抛物线交于A，C两点，其中C点的横坐标为2．
（1）求抛物线的解析式；
（2）求直线AC的函数表达式；
（3）若点M是线段AC上的点（不与A，C重合），过M作MF∥y轴交抛物线于F，交x轴于点H，设点M的横坐标为m，连接FA，FC，是否存在m，使△AFC的面积最大？若存在，求m的值；若不存在，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了这15人某月的加工零件个数：
每人加工零件个数
540
450
300
240
210
120
人数
1
1
2
6
3
2
(1)写出这15人该月加工零件数的平均数、中位数和众数．
(2)假如生产部负责人把每位工人的月加工零件个数定为260，你认为这个定额是否合理？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的方程x2﹣2（k﹣1）x+k2=0有两个实数根x1 ， x2 ．
（1）求k的取值范围；
（2）若|x1+x2|=x1x2﹣1，求k的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α，将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．
（1）求证：△COD是等边三角形；
（2）当α=150°时，试判断△AOD的形状，并说明理由．
相关试题
