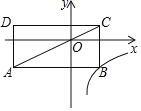
【题目】如图,在平面直角坐标系中,矩形ABCD的对角线AC经过坐标原点O,矩形的边分别平行于坐标轴,点B在函数![]() (k≠0,x>0)的图象上,点D的坐标为(﹣4,1),则k的值为( )
(k≠0,x>0)的图象上,点D的坐标为(﹣4,1),则k的值为( )
A.![]() B.
B.![]() C.4D.﹣4
C.4D.﹣4
参考答案:
【答案】D
【解析】
由于点B的坐标不能求出,但根据反比例函数的几何意义只要求出矩形OEBF的面积也可,依据矩形的性质发现S矩形OGDH=S矩形OEBF,而S矩形OGDH可通过点D(﹣4,1)转化为线段长而求得.,在根据反比例函数的所在的象限,确定k的值即可.
解:如图,根据矩形的性质可得:S矩形OGDH=S矩形OEBF,
∵D(﹣4,1),
∴OH=4,OG=1,
∴S矩形OGDH=OHOG=4,
设B(a,b),则OE=a,OF=﹣b,
∴S矩形OEBF,=OEOF=﹣ab=4,
又∵B(a,b)在函数![]() (k≠0,x>0)的图象上,
(k≠0,x>0)的图象上,
∴k=ab=﹣4
故选:D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】商人小周于上周买进某农场品10000
 ,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000
,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000 该品种的农产品,每个摊位的市场管理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况.
该品种的农产品,每个摊位的市场管理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况.星期
一
二
三
四
五
与前一天相比价格的涨跌情况/元
+0.3
-0.1
+0.25
+0.2
-0.5
当天的交易量/

2500
2000
3000
1500
1000
(1)星期四该农产品的价格为每千克多少元?
(2)本周内该农产品的最高价格为每千克多少元?最低价格为每千克多少元?
(3)小周在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,P为AB边上(不与A、B重合的一动点,过点P分别作PE⊥AC于点E,PF⊥BC于点F,则线段EF的最小值是( )
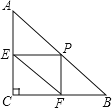

A. 2B. 3C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】张明暑假期间参加社会实践活动,从某批发市场以批发价每个m元的价格购进100个手机充电宝,然后每个加价n元到市场出售.
(1)求售出100个手机充电宝的总售价为多少元(结果用含m,n的式子表示)?
(2)由于开学临近,张明在成功售出60个充电宝后,决定将剩余充电宝按售价8折出售,并很快全部售完.
①她的总销售额是多少元?
②相比不采取降价销售,她将比实际销售多盈利多少元(结果用含m、n的式子表示)?
③若m=2n,张明实际销售完这批充电宝的利润率为 (利润率=利润÷进价×100%)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB和CD的公共部分BD=
 AB=
AB=  CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若AB=6,BC=4
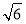 ,则FD=__________.
,则FD=__________.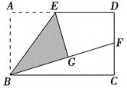
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形ABCD中,BD
 AD,延长AD至点E,使D是AE的中点,连接BE和CE,BE与CD交于点F.
AD,延长AD至点E,使D是AE的中点,连接BE和CE,BE与CD交于点F.(1)求证:四边形BDEC是矩形;
(2)若AB=6,AD=3,求矩形BDEC的面积.

相关试题

