【题目】如图,已知抛物线y=ax2+bx+3经过点B(﹣1,0)、C(3,0),交y轴于点A,将线段OB绕点O顺时针旋转90°,点B的对应点为点M,过点A的直线与x轴交于点D(4,0).直角梯形EFGH的上底EF与线段CD重合,∠FEH=90°,EF∥HG,EF=EH=1.直角梯形EFGH从点D开始,沿射线DA方向匀速运动,运动的速度为1个长度单位/秒,在运动过程中腰FG与直线AD始终重合,设运动时间为t秒.
(1)求此抛物线的解析式;
(2)当t为何值时,以M、O、H、E为顶点的四边形是特殊的平行四边形;
(3)作点A关于抛物线对称轴的对称点A′,直线HG与对称轴交于点K,当t为何值时,以A、A′、G、K为顶点的四边形为平行四边形?请直接写出符合条件的t值.
参考答案:
【答案】
(1)
解:∵抛物线y=ax2+bx+3经过点B(﹣1,0)、C(3,0),
∴ ![]() ,解得a=﹣1,b=2,
,解得a=﹣1,b=2,
∴抛物线的解析式为:y=﹣x2+2x+3.
(2)
解:在直角梯形EFGH运动的过程中:
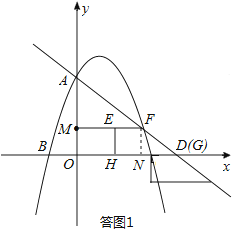
①四边形MOHE构成矩形的情形,如答图1所示:
此时边GH落在x轴上时,点G与点D重合.
由题意可知,EH,MO均与x轴垂直,且EH=MO=1,则此时四边形MOHE构成矩形.此时直角梯形EFGH平移的距离即为线段DF的长度.
过点F作FN⊥x轴于点N,则有FN=EH=1,FN∥y轴,
∴ ![]() ,即
,即 ![]() ,解得DN=
,解得DN= ![]() .
.
在Rt△DFN中,由勾股定理得:DF= ![]() =
= ![]() =
= ![]() ,
,
∴t= ![]() ;
;
②四边形MOHE构成正方形的情形.
由答图1可知,
OH=OD﹣DN﹣HN=4﹣ ![]() ﹣1=
﹣1= ![]() ,即OH≠MO,
,即OH≠MO,
所以此种情形不存在;
③四边形MOHE构成菱形的情形,如答图2所示:
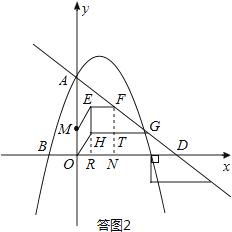
过点F作FN⊥x轴于点N,交GH于点T,过点H作HR⊥x轴于点R.易知FN∥y轴,RN=EF=FT=1,HR=TN.
设HR=x,则FN=FT+TN=FT+HR=1+x;
∵FN∥y轴,∴ ![]() ,即
,即 ![]() ,解得DN=
,解得DN= ![]() (1+x).
(1+x).
∴OR=OD﹣RN﹣DN=4﹣1﹣ ![]() (1+x)=
(1+x)= ![]() ﹣
﹣ ![]() x.
x.
若四边形MOHE构成菱形,则OH=EH=1,
在Rt△ORH中,由勾股定理得:OR2+HR2=OH2,
即:( ![]() ﹣
﹣ ![]() x)2+x2=12,解得x=
x)2+x2=12,解得x= ![]() ,
,
∴FN=1+x= ![]() ,DN=
,DN= ![]() (1+x)=
(1+x)= ![]() .
.
在Rt△DFN中,由勾股定理得:DF= ![]() =
= ![]() =3.
=3.
由此可见,四边形MOHE构成菱形的情形存在,此时直角梯形EFGH平移的距离即为线段DF的长度,
∴t=3.
综上所述,当t= ![]() s时,四边形MOHE构成矩形;当t=3s时,四边形MOHE构成菱形
s时,四边形MOHE构成矩形;当t=3s时,四边形MOHE构成菱形
(3)
解:当t= ![]() s或t=
s或t= ![]() s时,以A、A′、G、K为顶点的四边形为平行四边形.
s时,以A、A′、G、K为顶点的四边形为平行四边形.
简答如下:(注:本题并无要求写出解题过程,以下仅作参考)
由题意可知,AA′=2.以A、A′、G、K为顶点的四边形为平行四边形,则GK∥AA′,且GK=AA′=2.
①当直角梯形位于△OAD内部时,如答图3所示:
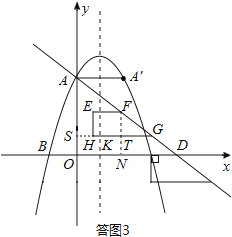
过点H作HS⊥y轴于点S,由对称轴为x=1可得KS=1,∴SG=KS+GK=3.
由SG∥x轴,得 ![]() ,求得AS=
,求得AS= ![]() ,∴OS=OA﹣AS=
,∴OS=OA﹣AS= ![]() ,
,
∴FN=FT+TN=FT+OS= ![]() ,易知DN=
,易知DN= ![]() FN=
FN= ![]() ,
,
在Rt△FND中,由勾股定理求得DF= ![]() ;
;
②当直角梯形位于△OAD外部时,如答图4所示:

设GK与y轴交于点S,则GS=SK=1,AS= ![]() ,OS=OA+AS=
,OS=OA+AS= ![]() .
.
过点F作FN⊥x轴,交GH于点T,则FN=FT+NT=FT+OS= ![]() .
.
在Rt△FGT中,FT=1,则TG= ![]() ,FG=
,FG= ![]() .
.
由TG∥x轴,∴ ![]() ,解得DF=
,解得DF= ![]() .
.
由于在以上两种情形中,直角梯形EFGH平移的距离均为线段DF的长度,则综上所述,当t= ![]() s或t=
s或t= ![]() s时,以A、A′、G、K为顶点的四边形为平行四边形.
s时,以A、A′、G、K为顶点的四边形为平行四边形.
【解析】(1)利用待定系数法求出抛物线的解析式;(2)在直角梯形的平移过程中,四边形MOHE可能构成矩形(如答图1所示),或菱形(如答图2所示);本问有两种情形,需要分类求解,注意不要漏解,而且需要排除正方形的情形;(3)本问亦有两种情形,需要分类求解.当直角梯形运动到△OAD内部的情形时,如答图3所示;当直角梯形运动到△OAD外部的情形时,如答图4所示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=16 km,CB=11 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣20+(﹣14)﹣(﹣18)﹣13 (2)27-18+43-32
(3)(+
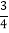 )﹣(﹣
)﹣(﹣ )﹣|﹣3| (4)
)﹣|﹣3| (4)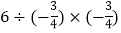
(5)﹣64÷3
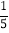 ×
× ; (6)∣-2∣
; (6)∣-2∣ 2+∣+7∣
2+∣+7∣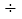 7+∣0∣
7+∣0∣(7)
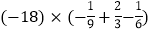 (8)
(8) 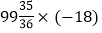
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,AB=AC.过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ,直线a交BC边于点P(点P不与点B、点C重合),△BMN的边MN始终在直线a上(点M在点N的上方),且BM=BN,连接CN.
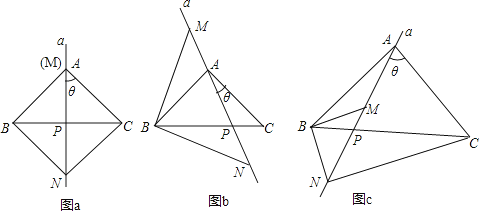
(1)当∠BAC=∠MBN=90°时,
①如图a,当θ=45°时,∠ANC的度数为△;
②如图b,当θ≠45°时,①中的结论是否发生变化?说明理由;
(2)如图c,当∠BAC=∠MBN≠90°时,请直接写出∠ANC与∠BAC之间的数量关系,不必证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】生活与数学
(1)吉姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是32,那么第一个数是 ;

(2)玛丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是42,则它们分别是 ;

(3)莉莉也在日历上圈出5个数,呈十字框形,它们的和是50,则中间的数是 ;

(4)某月有5个星期日的和是75,则这个月中最后一个星期日是 号;
(5)若干个偶数按每行8个数排成下图:
①图中方框内的9个数的和与中间的数的关系是 ;

②汤姆所画的斜框内9个数的和为360,则斜框的中间一个数是 ;

③托马斯也画了一个斜框,斜框内9个数的和为252,则斜框的中间一个数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)点A,B在数轴上分别表示有理数a,b,A,B两点之间的距离表示为AB,在数轴上A,B两点距离AB=|a﹣b|.已知数轴上两点A,B对应的数分别为-1,3.点P为数轴上一动点,其对应的数为x,A,B两点之间的距离是 .设点P在数轴上表示的数为x,则x与-4之间的距离表示为 .
.若点P到点A、点B的距离相等,则点P对应的数为 .
若点P到点A、点B的距离之和为8,则点P对应的数为 .
现在点A以2个单位长度/秒的速度向右运动,同时点B以0.5个单位长度/秒的速度向左运动,当点A与点B之间的距离为3个单位长度时,求点A所对应的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(﹣1,0),下面的四个结论:①OA=3;②a+b+c<0;③ac>0;④b2﹣4ac>0.其中正确的结论是( )
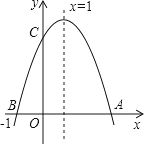
A.①④
B.①③
C.②④
D.①②
相关试题

