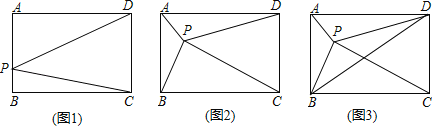
【题目】四边形![]() 是长方形,面积为
是长方形,面积为![]()
(1)如图1,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() 、
、![]() ,则三角形
,则三角形![]() 的面积为 (用含
的面积为 (用含![]() 的代数式表示).
的代数式表示).
(2)![]() 是长方形
是长方形![]() 内一点,连接
内一点,连接![]() 、
、![]() 、
、![]() 、
、![]() ,三角形
,三角形![]() 的面积为
的面积为![]() .
.
①如图2,则三角形![]() 的面积为 ;(用含
的面积为 ;(用含![]() 、
、![]() 的代数式表示)
的代数式表示)
②如图3,连接![]() ,若三角形
,若三角形![]() 的面积为
的面积为![]() ,则三角形
,则三角形![]() 的面积为 .(用含
的面积为 .(用含![]() 的代数式表示)
的代数式表示)
参考答案:
【答案】(1)![]() m;(2)①
m;(2)①![]() ma;②ba
ma;②ba
【解析】
(1)根据△PCD的面积等于矩形的面积的一半计算即可.
(2)①根据△CPD的面积为长方形面积的一半减去△ABP的面积可得;
②根据△BPC的面积等于△APD的面积进行解答即可.
解:(1)如图1中,过点P作PM⊥CD于点M,
∵四边形ABCD是矩形,
∴AB=CD,AD=BC=PM,
∴S△PCD=![]() S矩形ABCD=
S矩形ABCD=![]() m.
m.
故答案为:![]() m;
m;
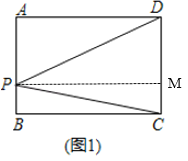
(2)①如图2中,作PE⊥AB于E交CD于F.
∵S△PAB+S△PCD=![]() ABPE+
ABPE+![]() CDPF=
CDPF=![]() AB(PE+PF)=
AB(PE+PF)=![]() ABEF=
ABEF=![]() m,
m,
S△PAB=a,
∴S△PCD=![]() ma
ma
故答案为:![]() ma.
ma.

②如图3中,
∵S△PBD=S△PBC+S△PCDS△BCD,
∴S△PBD=b+![]() ma
ma![]() m=ba.
m=ba.
故答案为:ba.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:
 ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1: 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:
 1.414,
1.414, 1.732)
1.732) -
科目: 来源: 题型:
查看答案和解析>>【题目】(问题情境)学习《探索全等三角形条件》后,老师提出了如下问题:如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围。同学通过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.根据SAS可证得到△ADC≌△EDB,从而根据“三角形的三边关系”可求得AD的取值范围是 。解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
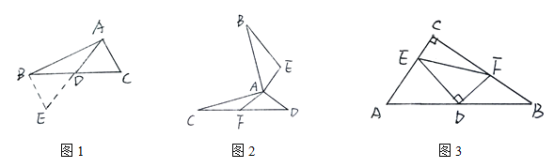
(直接运用)如图②,AB⊥AC,AD⊥AE,AB=AC,AD=AE,AF是ACD的边CD上中线.求证:BE=2AF.
(灵活运用)如图③,在△ABC中,∠C=90°,D为AB的中点,DE⊥DF,DE交AC于点E,DF交AB于点F,连接EF,试判断以线段AE、BF、EF为边的三角形形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲.乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠一盒乒乓球;乙店的优惠办法是:按定价的9折出售.某班需购买乒乓球拍4副,乒乓球若干盒(不少于4盒).
(1)用代数式表示(所填式子需化简):当购买乒乓球的盒数为
 盒时,在甲店购买需付款 元;在乙店购买需付款 元.
盒时,在甲店购买需付款 元;在乙店购买需付款 元.(2)当购买乒乓球盒数为10盒时,到哪家商店购买比较合算?说出你的理由.
(3)当购买乒乓球盒数为10盒时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付款几元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
(1)如图a,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
① 如图b,求证:BE⊥DQ;
② 如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由;
③ 若正方形ABCD的边长为10,DE=2,PB=PC,直接写出线段PB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上
 点表示数
点表示数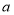 ,
,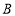 点表示数
点表示数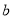 ,
, 表示
表示 点和
点和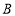 点之间的距离,且
点之间的距离,且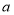 、
、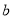 满足
满足 数轴上有一动点
数轴上有一动点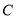 ,从
,从 点出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为
点出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为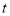 秒
秒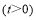 ,
,
(1)点
 表示的数为 ,点
表示的数为 ,点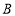 表示的数为 .
表示的数为 .(2)点
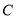 表示的数 (用含
表示的数 (用含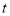 的代数式表示);
的代数式表示);(3)当点
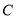 运动 秒时,点
运动 秒时,点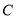 和点
和点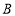 之间距离为4;
之间距离为4;(4)若数轴上另有一动点
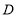 ,同时从
,同时从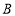 点出发,以每秒1个单位长度的速度沿数轴向左匀速运动,当点
点出发,以每秒1个单位长度的速度沿数轴向左匀速运动,当点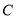 和点
和点 之间距离为6时,求时间
之间距离为6时,求时间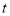 的值.
的值. -
科目: 来源: 题型:
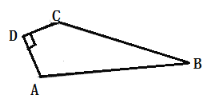
查看答案和解析>>【题目】如图,所是一块草坪已知:AD=12m,CD=9m,∠ADC=90°,AB=39m, BC=36m,求这块草坪的面积.
相关试题

