【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
(1)如图a,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
① 如图b,求证:BE⊥DQ;
② 如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由;
③ 若正方形ABCD的边长为10,DE=2,PB=PC,直接写出线段PB的长.

参考答案:
【答案】(1)证明见解析;(2)①证明见解析;②△DEP为等腰直角三角形,证明见解析;③PB=![]() 或
或![]()
【解析】(1)由旋转的性质得到∠BCP=∠DCQ,即可证明△BCP≌△DCQ;
(2)①由全等的性质和对顶角相等即可得到答案;
②由等边三角形的性质和旋转的性质求出∠EPD=45°,∠EDP=45°,即可判断△DEP的形状.
③由(1)结论,根据等腰三角形三线合一性质和相似三角形性质及勾股定理可得.
(1):如图a
证明:∵∠BCD=90°,∠PCQ=90°,
∴∠BCP=∠DCQ,
在△BCP和△DCQ中,
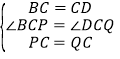 ,
,
∴△BCP≌△DCQ
(2)①如图b,∵△BCP≌△DCQ,
∴∠CBF=∠EDF,又∠BFC=∠DFE,
∴∠DEF=∠BCF=90°,
∴BE⊥DQ;
②△DEP为等腰直角三角形
∵△BCP为等边三角形,
∴∠BCP=60°,∴∠PCD=30°,又CP=CD,
∴∠CPDF=∠CDP=75°,又∠BPC=60°,∠CDQ=60°,
∴∠EPD=45°,∠EDP=45°,
∴△DEP为等腰直角三角形.
③PB= ![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题情境)学习《探索全等三角形条件》后,老师提出了如下问题:如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围。同学通过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.根据SAS可证得到△ADC≌△EDB,从而根据“三角形的三边关系”可求得AD的取值范围是 。解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
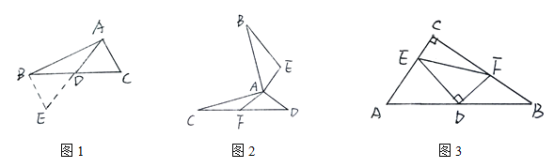
(直接运用)如图②,AB⊥AC,AD⊥AE,AB=AC,AD=AE,AF是ACD的边CD上中线.求证:BE=2AF.
(灵活运用)如图③,在△ABC中,∠C=90°,D为AB的中点,DE⊥DF,DE交AC于点E,DF交AB于点F,连接EF,试判断以线段AE、BF、EF为边的三角形形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲.乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠一盒乒乓球;乙店的优惠办法是:按定价的9折出售.某班需购买乒乓球拍4副,乒乓球若干盒(不少于4盒).
(1)用代数式表示(所填式子需化简):当购买乒乓球的盒数为
 盒时,在甲店购买需付款 元;在乙店购买需付款 元.
盒时,在甲店购买需付款 元;在乙店购买需付款 元.(2)当购买乒乓球盒数为10盒时,到哪家商店购买比较合算?说出你的理由.
(3)当购买乒乓球盒数为10盒时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付款几元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
 是长方形,面积为
是长方形,面积为
(1)如图1,
 是
是 边上一点,连接
边上一点,连接 、
、 ,则三角形
,则三角形 的面积为 (用含
的面积为 (用含 的代数式表示).
的代数式表示).(2)
 是长方形
是长方形 内一点,连接
内一点,连接 、
、 、
、 、
、 ,三角形
,三角形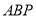 的面积为
的面积为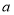 .
.①如图2,则三角形
 的面积为 ;(用含
的面积为 ;(用含 、
、 的代数式表示)
的代数式表示)②如图3,连接
 ,若三角形
,若三角形 的面积为
的面积为 ,则三角形
,则三角形 的面积为 .(用含
的面积为 .(用含 的代数式表示)
的代数式表示)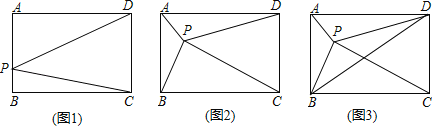
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上
 点表示数
点表示数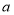 ,
,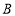 点表示数
点表示数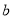 ,
, 表示
表示 点和
点和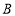 点之间的距离,且
点之间的距离,且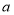 、
、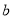 满足
满足 数轴上有一动点
数轴上有一动点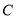 ,从
,从 点出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为
点出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为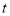 秒
秒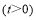 ,
,
(1)点
 表示的数为 ,点
表示的数为 ,点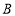 表示的数为 .
表示的数为 .(2)点
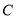 表示的数 (用含
表示的数 (用含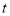 的代数式表示);
的代数式表示);(3)当点
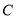 运动 秒时,点
运动 秒时,点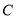 和点
和点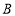 之间距离为4;
之间距离为4;(4)若数轴上另有一动点
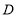 ,同时从
,同时从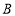 点出发,以每秒1个单位长度的速度沿数轴向左匀速运动,当点
点出发,以每秒1个单位长度的速度沿数轴向左匀速运动,当点 和点
和点 之间距离为6时,求时间
之间距离为6时,求时间 的值.
的值. -
科目: 来源: 题型:
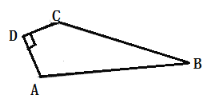
查看答案和解析>>【题目】如图,所是一块草坪已知:AD=12m,CD=9m,∠ADC=90°,AB=39m, BC=36m,求这块草坪的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件:①∠A+∠B=∠C,②∠C=90°,③AC:BC:AB=3:4:5,④∠A:∠B:∠C=3:4:5.⑤a2=(b+c)(b﹣c)中,能确定△ABC是直角三角形的有( )
A.2个B.3个C.4个D.5个
相关试题

