【题目】如图1,对于平面直角坐标系x O y中的点A和点P,若将点P绕点A顺时针旋转90°后得到点Q,则称点Q为点P关于点A的“垂链点”.


(1) △PAQ是__________三角形;
(2)已知点A的坐标为(0, 0),点P关于点A的“垂链点”为点Q
①若点P的坐标为(2, 0),则点Q的坐标为___________;
②若点Q的坐标为(-2, 1),则点P的坐标为___________;
(3)如图2, 已知点D的坐标为(3, 0),点C在直线y=2x上,若点C关于点D的“垂链点”在坐标轴上,试求点C的坐标.
参考答案:
【答案】(1)等腰直角;(2)①(0, -2);②(-1, -2);(3)点C坐标(3,6)或(![]() , -3).
, -3).
【解析】
(1)根据旋转的性质,得到AP=AQ,∠PAQ=90°,即可得到答案;
(2)根据旋转的性质和“垂链点”的定义,分别求出点Q和点P的坐标即可;
(3)①当点C在第一象限时,则点C关于点D的“垂链点”在x轴上,则CD⊥x轴,即可求解;②当点C在第三象限时,证明△CDH≌△DOC1(AAS),得到CH=OD=3,即可求出点C的坐标.
解:(1)由旋转的性质,可知,AP=AQ,∠PAQ=90°,
∴△PAQ是等腰直角三角形;
故答案为:等腰直角;
(2)∵点A为(0,0),即为原点,
根据旋转的性质和“垂链点”的定义,得
①若点P的坐标为(2,0),则点Q的坐标为(![]() );
);
②点Q的坐标为(![]() ,1),则点P的坐标为(
,1),则点P的坐标为(![]() );
);
故答案为:①(![]() );②(
);②(![]() );
);
(3)根据题意,点D为(3,0);
①当点C在第一象限时,则点C关于点D的“垂链点”在x轴上,
∴CD⊥x轴,
∴点C的横坐标为3,
∵点C在直线y=2x上,则y=6,
∴点C的坐标为:(3,6);
②当点C在第三象限时,则“垂链点”C1在y轴上,
过点C作CH⊥x轴,交点为H,如图:

∵CH⊥x轴,∠CDC1=90°,
∴∠CHD=∠DOC1=90°,
∴∠CDH+∠HDC1=∠CDC1=90°,∠HDC1+∠OC1D=90°,
∴∠CDH=∠OC1D,
∵CD=C1D,
∴△CDH≌△DOC1(AAS),
∴CH=OD=3,
∴点C的纵坐标为![]() ,
,
把![]() 代入y=2x,解得:
代入y=2x,解得:![]() ,
,
∴点C的坐标为:(![]() ,
,![]() );
);
综合上述,点C的坐标为:(3,6)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】具备下列各组条件的两个三角形中,不一定相似的是( )
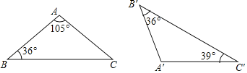
A. 有一个角是
 的两个等腰三角形 B. 有一个角为
的两个等腰三角形 B. 有一个角为 的两个等腰三角形
的两个等腰三角形C. 有一锐角对应相等的两个直角三角形 D. 图中的
 与
与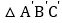 相似
相似 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形
 的边长为
的边长为 ,
, 是
是 的中点,过点
的中点,过点 作
作 ,交
,交 于点
于点 ,连接
,连接 并延长,交
并延长,交 的延长线于点
的延长线于点 .则
.则 的长为( )
的长为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 、
、 两点分别在边
两点分别在边 、
、 上,
上, ,
,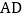 与
与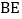 相交于点
相交于点 ,若
,若 的面积为
的面积为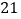 ,则
,则 的面积为________.
的面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是等腰
是等腰 的斜边
的斜边 上的一点,
上的一点, ,
, 于点
于点 交
交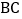 于点
于点 .
.
 求证:
求证: 是
是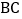 的中点;
的中点; 求
求 的值;
的值; 求
求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形ABC中,∠BCA=90
 ,∠A=60
,∠A=60 ,CD是角平分线,在CB上截取CE=CA.
,CD是角平分线,在CB上截取CE=CA.求证:⑴ DE=BE;
⑵ 若AC=1,AD=
 ,试求△ABC的面积.
,试求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店用1000元人民币购进水果销售,过了一段时间又用2800元购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次购进的贵了2元.
(1)求该商店第一次购进水果多少千克?
(2)该商店两次购进的水果按照相同的标价销售一段时间后,将最后剩下的100千克按照标价的半价出售.售完全部水果后,利润不低于1700元,则最初每千克水果的标价至少是多少?
相关试题

