【题目】如图,点![]() 是等腰
是等腰![]() 的斜边
的斜边![]() 上的一点,
上的一点,![]() ,
,![]() 于点
于点![]() 交
交![]() 于点
于点![]() .
.

![]() 求证:
求证:![]() 是
是![]() 的中点;
的中点;
![]() 求
求![]() 的值;
的值;
![]() 求
求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析(2)2(3)![]()
【解析】
(1)作BP⊥BC交CD的延长线于P,如图1,先由AC∥BP得![]() ,由于AB=3BD,则AD=2BD,AC=2BP,所以BC=2BP,再证明△ACE≌△CBP得到CE=BP,则BC=2CE,于是可判断E是BC的中点;
,由于AB=3BD,则AD=2BD,AC=2BP,所以BC=2BP,再证明△ACE≌△CBP得到CE=BP,则BC=2CE,于是可判断E是BC的中点;
(2)证明Rt△ACF∽△CEF,则![]() ,而BC=AC=2CE,易得
,而BC=AC=2CE,易得![]() =2;
=2;
(3)作DH∥AE交BC于H,如图2,根据平行线分线段成比例定理得![]() ,则EH=
,则EH=![]() BE,再由EF∥DH,然后利用平行线分线段成比例定理即可得到
BE,再由EF∥DH,然后利用平行线分线段成比例定理即可得到![]() =
=![]() .
.
![]() 证明:作
证明:作![]() 交
交![]() 的延长线于
的延长线于![]() ,如图
,如图![]() ,
,
∵![]() ,
,

∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,

而![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的中点;
的中点;![]() 解:∵
解:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() ;
;![]() 解:作
解:作![]() 交
交![]() 于
于![]() ,如图
,如图![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形
 的边长为
的边长为 ,
, 是
是 的中点,过点
的中点,过点 作
作 ,交
,交 于点
于点 ,连接
,连接 并延长,交
并延长,交 的延长线于点
的延长线于点 .则
.则 的长为( )
的长为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 、
、 两点分别在边
两点分别在边 、
、 上,
上, ,
,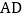 与
与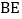 相交于点
相交于点 ,若
,若 的面积为
的面积为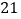 ,则
,则 的面积为________.
的面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,对于平面直角坐标系x O y中的点A和点P,若将点P绕点A顺时针旋转90°后得到点Q,则称点Q为点P关于点A的“垂链点”.


(1) △PAQ是__________三角形;
(2)已知点A的坐标为(0, 0),点P关于点A的“垂链点”为点Q
①若点P的坐标为(2, 0),则点Q的坐标为___________;
②若点Q的坐标为(-2, 1),则点P的坐标为___________;
(3)如图2, 已知点D的坐标为(3, 0),点C在直线y=2x上,若点C关于点D的“垂链点”在坐标轴上,试求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形ABC中,∠BCA=90
 ,∠A=60
,∠A=60 ,CD是角平分线,在CB上截取CE=CA.
,CD是角平分线,在CB上截取CE=CA.求证:⑴ DE=BE;
⑵ 若AC=1,AD=
 ,试求△ABC的面积.
,试求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店用1000元人民币购进水果销售,过了一段时间又用2800元购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次购进的贵了2元.
(1)求该商店第一次购进水果多少千克?
(2)该商店两次购进的水果按照相同的标价销售一段时间后,将最后剩下的100千克按照标价的半价出售.售完全部水果后,利润不低于1700元,则最初每千克水果的标价至少是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.
⑴如图1,若∠BAC=60°,求证:△CEF是等边三角形.
⑵若∠BAC<60°.
①如图2,当点D在线段CB上移动时,判断△CEF为等腰三角形并证明;
②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请你在图3中画出相应的图形并直接写出结论(不必证明).

相关试题

