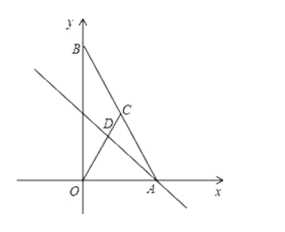
【题目】如图,在平面直角坐标系中,![]() 为直线
为直线![]() 与直线
与直线![]() 的交点,点
的交点,点![]() 在线段
在线段![]() 上,
上,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若![]() 为线段
为线段![]() 上一动点(不与
上一动点(不与![]() 重合),
重合),![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,请求出
,请求出![]() 与
与![]() 的函数关系式;
的函数关系式;
参考答案:
【答案】(1)![]() ;(2)S=
;(2)S=![]() .
.
【解析】
(1)先利用A,B坐标求出直线AB的解析式,再求出与直线y=2x的交点坐标C即可;(2)设D(t,2t)利用勾股定理求出D(1,2),再求出AD的解析式为:y=-x+3,由P(x,-x+3),再求出S△POD的函数关系式;
(1)∵A的坐标是(3,0),B(0,6)
∴直线AB的解析式y=-2x+6
∵C为直线y=2x与直线AB的交点,
∴![]() 解得
解得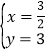
∴C![]() ;
;
(2)设D(t,2t)
∵t2+4t2=5
∴t=1
故D(1,2)
AD的解析式为:y=-x+3
P(x,-x+3)
∴S△POD=![]() =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】任意写出一个数位不含零的三位数,任取三个数字中的两个,组合成所有可能的两位数(有6个),求出所有这些两位数的和,然后将它除以原三位数的各个数位上的数的和.例如,对三位数223,取其两个数字组成所有可能的两位数:22,23,22,23,32,32.它们的和是154.三位数223各位数的和是7,
 再换几个数试一试,你发现了什么?请写出你按上面方法的探索过程和所发现的结果,并运用代数式的知识说明所发现的结果的正确性.
再换几个数试一试,你发现了什么?请写出你按上面方法的探索过程和所发现的结果,并运用代数式的知识说明所发现的结果的正确性. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
(2)如图2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 开通了,中国联通公布了资费标准,其中包月
开通了,中国联通公布了资费标准,其中包月 元时,超出部分国内拨打
元时,超出部分国内拨打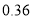 元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.时间/分
1
2
3
4
5
…
电话费/元
0.36
0.72
1.08
1.44
1.80
…
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用
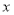 表示超出时间,
表示超出时间,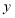 表示超出部分的电话费,那么
表示超出部分的电话费,那么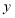 与
与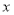 的关系式是什么?
的关系式是什么?(3)如果打电话超出
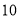 分钟,需多付多少电话费?
分钟,需多付多少电话费?(4)某次打电话的费用超出部分是
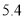 元,那么小明的爸爸打电话超出几分钟?
元,那么小明的爸爸打电话超出几分钟? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是直径,P为AB上一点,过点P作弦MN,∠NPB=45°.
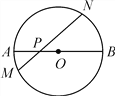
(1)若AP=2,BP=6,求MN的长;
(2)若MP=3,NP=5,求AB的长;
(3)若⊙O的半径为R,求PM2+PN2的值.
-
科目: 来源: 题型:
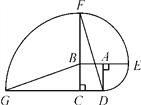
查看答案和解析>>【题目】如图,四边形ABCD是边长为1的正方形,其中
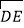 ,
,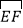 ,
,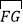 的圆心依次是点A,B,C.
的圆心依次是点A,B,C.(1)求点D沿三条圆弧运动到点G所经过的路线长;
(2)判断直线GB与DF的位置关系,并说明理由.
相关试题

