【题目】在平面直角坐标系中,△ABC的三个顶点的坐标为A(3,4),B(1,2), C(5, 1).
(1)写出A、B、C关于y轴对称的点A1、B1、C1的坐标: A1_____、 B1 、C1 ;
(2)若![]() 各顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点A'、B'、C',并依次连接这三个点,判断所得△A′B′C′与原
各顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点A'、B'、C',并依次连接这三个点,判断所得△A′B′C′与原![]() 有怎样的位置关系。
有怎样的位置关系。

参考答案:
【答案】(1)(-3,4),(-1,2),(-5,1);(2)作出![]() 见解析.与原
见解析.与原![]() 的位置关系是关于x轴对称
的位置关系是关于x轴对称
【解析】
(1)根据轴对称的性质,找到A、B、C关于y轴对称的A1、B1、C1,写出各点坐标即可;
(2)根据纵坐标乘以-1,得到A'、B'、C'的坐标,然后画出图形,判断与原图形的关系即可.
解:(1)根据关于y轴对称的点坐标性质,得:A1 (-3,4),B1(-1,2),C1(-5,1);
故答案为:(-3,4),(-1,2),(-5,1);
(2)如图所示,
A'为(3,-4),B'为(1,-2),C'(5,-1);

∴![]() 与原
与原![]() 的位置关系是关于x轴对称
的位置关系是关于x轴对称
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经销水杯,电热水壶两种商品,水杯每个进价15元,售价20元;电热水壶每个进价35元,售价45元.
(1)若该商场同时购进水杯、电热水壶共100件,恰好用去2700元,求能购进水杯、电热水壶各多少个?
(2)商场要求小明用1050元的钱(必须全部用完)采购水杯、电热水壶(或其中一种商品),且还要求总利润不少于340元(假设商品全部卖完),请你确定所有的进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明用大小相同高度为2cm的10块小长方体垒了两堵与地面垂直的木墙AD, BE,当他将一个等腰直角三角板ABC如图垂直放入时,直角顶点C正好在水平线DE上,锐角顶点A和B分别与木墙的顶端重合,求两堵木墙之间的距离。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知ABCD的周长为26,∠ABC=120°,BD为一条对角线,⊙O内切于△ABD,E,F,G为切点,已知⊙O的半径为
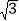 .求ABCD的面积.
.求ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程mx2+(1﹣5m)x﹣5=0(m≠0).
(1)求证:无论m为任何非零实数,此方程总有两个实数根;
(2)若抛物线y=mx2+(1﹣5m)x﹣5与x轴交于A(x1,0)、B(x2,0)两点,且|x1﹣x2|=6,求m的值;
(3)若m>0,点P(a,b)与Q(a+n,b)在(2)中的抛物线上(点P、Q不重合),求代数式4a2﹣n2+8n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,实线部分是由正方形,正五边形和正六边形叠放在一起形成的,其中正方形和正六边形的边长相同,求图中∠MON的度数.
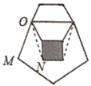
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,BC=1,
中,BC=1, .
.
(1)求AB的长度:
(2)过点A作AB的垂线,交AC的垂直平分线于点D ,以AB为一边作等边
 .
.①连接CE,求证: BD=CE;
②连接DE交AB于F.求
 的值.
的值.
相关试题

