搜索
【题目】已知ABCD的周长为26，∠ABC=120°，BD为一条对角线，⊙O内切于△ABD，E，F，G为切点，已知⊙O的半径为
．求ABCD的面积．
参考答案：
【答案】20
【解析】
首先利用三边及⊙O的半径表示出平行四边形的面积，再根据题意求出AB+AD=13，然后利用切线的性质求出BD的长即可解答.
设⊙O分别切△ABD的边AD、AB、BD于点G、E、F；
平行四边形ABCD的面积为S；
则S=2S△ABD=2×
(AB·OE+BD·OF+AD·OG)=（AB+AD+BD）；
∵平行四边形ABCD的周长为26，
∴AB+AD=13，
∴S=(13+BD)；连接OA；
由题意得：∠OAE=30°，
∴AG=AE=3；同理可证DF=DG，BF=BE；
∴DF+BF=DG+BE=13﹣3﹣3=7，
即BD=7，
∴S=（13+7）=20．
即平行四边形ABCD的面积为20．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校“体育课外活动兴趣小组”，开设了以下体育课外活动项目：A．足球 B．乒乓球C．羽毛球 D．篮球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：
（1）这次被调查的学生共有 人，在扇形统计图中“D”对应的圆心角的度数为 ；
（2）请你将条形统计图补充完整；
（3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加市里组织的乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场经销水杯，电热水壶两种商品，水杯每个进价15元，售价20元；电热水壶每个进价35元，售价45元．
（1）若该商场同时购进水杯、电热水壶共100件，恰好用去2700元，求能购进水杯、电热水壶各多少个？
（2）商场要求小明用1050元的钱（必须全部用完）采购水杯、电热水壶（或其中一种商品），且还要求总利润不少于340元（假设商品全部卖完），请你确定所有的进货方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明用大小相同高度为2cm的10块小长方体垒了两堵与地面垂直的木墙AD， BE，当他将一个等腰直角三角板ABC如图垂直放入时，直角顶点C正好在水平线DE上，锐角顶点A和B分别与木墙的顶端重合，求两堵木墙之间的距离。
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，△ABC的三个顶点的坐标为A(3，4)，B(1，2)， C(5， 1).
(1)写出A、B、C关于y轴对称的点A1、B1、C1的坐标: A1_____、 B1 、C1 ；
(2)若
各顶点的横坐标不变，纵坐标都乘以-1，请你在同一坐标系中描出对应的点A'、B'、C'，并依次连接这三个点，判断所得△A′B′C′与原有怎样的位置关系。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的一元二次方程mx2+（1﹣5m）x﹣5=0（m≠0）．
（1）求证：无论m为任何非零实数，此方程总有两个实数根；
（2）若抛物线y=mx2+（1﹣5m）x﹣5与x轴交于A（x1，0）、B（x2，0）两点，且|x1﹣x2|=6，求m的值；
（3）若m＞0，点P（a，b）与Q（a+n，b）在（2）中的抛物线上（点P、Q不重合），求代数式4a2﹣n2+8n的值．
-
科目： 来源： 题型：
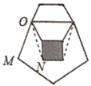
查看答案和解析>>【题目】如图，实线部分是由正方形，正五边形和正六边形叠放在一起形成的，其中正方形和正六边形的边长相同，求图中∠MON的度数.
相关试题
