【题目】如图直线l:y=kx+6与x轴、y轴分别交于点B、C两点,点B的坐标是(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值.
(2)若点P是直线l在第二象限内一个动点,当点P运动到什么位置时,△PAC的面积为3,求出此时直线AP的解析式.
(3)在x轴上是否存在一点M,使得△BCM为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ,(2)P(﹣4,3);y=
,(2)P(﹣4,3);y=![]() x+9.(3)(﹣18,0),(﹣
x+9.(3)(﹣18,0),(﹣![]() ,0),(2,0)或(8,0),见解析.
,0),(2,0)或(8,0),见解析.
【解析】
(1)由点B的坐标,利用一次函数图象上点的坐标特征可求出k值;
(2)利用一次函数图象上点的坐标特征求出点C的坐标,设点P的坐标为(x,![]() x+6),由S△PAC=S△BOC﹣S△BAP﹣S△AOC结合△PAC的面积为3,可得出关于x的一元一次方程,解之即可得出点P的坐标,再利用待定系数法即可求出此时直线AP的解析式;
x+6),由S△PAC=S△BOC﹣S△BAP﹣S△AOC结合△PAC的面积为3,可得出关于x的一元一次方程,解之即可得出点P的坐标,再利用待定系数法即可求出此时直线AP的解析式;
(3)利用勾股定理求出BC的长度,分CB=CM,BC=BM,MB=MC三种情况考虑:①当CB=CM时,由OM1=OB=8可得出点M1的坐标;②当BC=BM时,由BM2=BM3=BC=10结合点B的坐标可得出点M2,M3的坐标;③当MB=MC时,设OM=t,则M4B=M4C=8﹣t,利用勾股定理可得出关于t的一元一次方程,解之即可得出点M4的坐标.综上,此题得解.
(1)∵直线l:y=kx+6过点B(﹣8,0),
∴0=﹣8k+6,
∴k=![]() .
.
(2)当x=0时,y=![]() x+6=6,
x+6=6,
∴点C的坐标为(0,6).
依照题意画出图形,如图1所示,
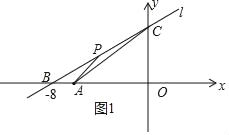
设点P的坐标为(x,![]() x+6),
x+6),
∴S△PAC=S△BOC﹣S△BAP﹣S△AOC,
=![]() ×8×6﹣
×8×6﹣![]() ×2(
×2(![]() x+6)﹣
x+6)﹣![]() ×6×6,
×6×6,
=﹣![]() x=3,
x=3,
∴x=﹣4,
∴点P的坐标为(﹣4,3).
设此时直线AP的解析式为y=ax+b(a≠0),
将A(﹣6,0),P(﹣4,3)代入y=ax+b,
得:![]() ,解得:
,解得: ,
,
∴当点P的坐标为(﹣4,3)时,△PAC的面积为3,此时直线AP的解析式为y=![]() x+9.
x+9.
(3)在Rt△BOC中,OB=8,OC=6,
∴BC=![]() =10.
=10.
分三种情况考虑(如图2所示):
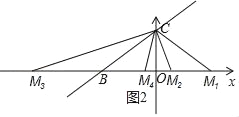
①当CB=CM时,OM1=OB=8,
∴点M1的坐标为(8,0);
②当BC=BM时,BM2=BM3=BC=10,
∵点B的坐标为(﹣8,0),
∴点M2的坐标为(2,0),点M3的坐标为(﹣18,0);
③当MB=MC时,设OM=t,则M4B=M4C=8﹣t,
∴CM42=OM42+OC2,即(8﹣t)2=t2+62,
解得:t=![]() ,
,
∴点M4的坐标为(﹣![]() ,0).
,0).
综上所述:在x轴上存在一点M,使得△BCM为等腰三角形,点M的坐标为(﹣18,0),(﹣![]() ,0),(2,0)或(8,0).
,0),(2,0)或(8,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点(﹣2,5),并且与y轴交于点P,直线y=
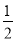 x+3与y轴交于点Q,点Q恰与点P关于x轴对称,求这个一次函数的解析式.
x+3与y轴交于点Q,点Q恰与点P关于x轴对称,求这个一次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校课程安排中,各班每天下午只安排三节课.
(1)初一(1)班星期二下午安排了数学、英语、生物课各一节,通过画树状图求出把数学课安排在最后一节的概率;
(2)星期三下午,初二(1)班安排了数学、物理、政治课各一节,初二(2)班安排了数学、语文、地理课各一节,此时两班这六节课的每一种课表排法出现的概率是
 .已知这两个班的数学课都由同一个老师担任,其他课由另外四位老师担任.求这两个班数学课不相冲突的概率.
.已知这两个班的数学课都由同一个老师担任,其他课由另外四位老师担任.求这两个班数学课不相冲突的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行以“助人为乐,乐在其中”为主题的演讲比赛,比赛设一个第一名,一个第二名,两个并列第三名.前四名中七、八年级各有一名同学,九年级有两名同学,小蒙同学认为前两名是九年级同学的概率是
 ,你赞成他的观点吗?请用列表法或画树形图法分析说明.
,你赞成他的观点吗?请用列表法或画树形图法分析说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA,PB是⊙O的切线,A,B是切点,点C是劣弧AB上的一点,若∠P=40°,则∠ACB等于( )

A. 80° B. 110° C. 120° D. 140°
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从相距420km的A、B两地相向而行,乙车比甲车先出发1小时,两车分别以各自的速度匀速行驶,途经C地(A、B、C三地在同一条直线上).甲车到达C地后因有事立即按原路原速返回A地,乙车从B地直达A地,甲、乙两车距各自出发地的路程y(千米)与甲车行驶所用的时间x(小时)的关系如图所示,结合图象信息回答下列问题:
(1)甲车的速度是 千米/时,乙车的速度是 千米/时;
(2)求甲车距它出发地的路程y(千米)与它行驶所用的时间x(小时)之间的函数关系式;
(3)甲车出发多长时间后两车相距90千米?请你直接写出答案.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在圆⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为( )

A. 19 B. 16 C. 18 D. 20
相关试题

