【题目】数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.在数轴上若点A、B分别表示有理数a、b ,在数轴上A、B两点之间的距离AB=| a-b | .结合数轴与绝对值的知识回答下列问题:
![]()
(1)数轴上表示﹣3和2的两点之间的距离是_____;数轴上表示 x 和 -3 两点之间的距离是_____;
(2)若a表示一个有理数,则|a+4|+|a﹣2|有最小值吗?若有,请求出最小值;若没有,请说明理由;
(3)当a =_____时,|a+4|+|a﹣1|+|a﹣2|的值最小,最小值是_____.
参考答案:
【答案】(1)5, ![]() ;(2) 有,最小值是6; (3) 1, 6
;(2) 有,最小值是6; (3) 1, 6
【解析】
(1)直接根据数轴上A、B两点之间的距离|AB|=|a-b|.代入数值运用绝对值即可求任意两点间的距离.
(2)代数式|a+4|+|a﹣2|表示数轴上一点到4、-2两点的距离的和,根据两点之间线段最短,进而得出答案.
(3)依据绝对值的几何意义回答即可.
解:(1)数轴上表示-3和2的两点之间的距离是|-3-2|=5,数轴上表示x和-3的两点之间的距离是|x-(-3)|=![]() .
.
(2)代数式|a+4|+|a﹣2|表示数轴上一点a到-4和2两点的距离和,根据两点之间线段最短可知,有最小值为:2-(-4)=6.
(3)①当a≤-4时,原式=-a-4-a+1-a+2 =-3a-1,a=-4时,最小值为11;
②当-4<a≤1时,原式=a+4-a+1-a+2=-a+7,a=1时,最小值为6;
③当1<a≤2时,原式=a+4+a-1-a+2=a+5,a=1时,最小值为6;
④当a>2时,原式=a+4+a-1+a-2=3a+1,a=2时,最小值为7;
综上,当a =1时,|a+4|+|a﹣1|+|a﹣2|的值最小,最小值是6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD⊥AC,AB=6,AC=5
 ,∠A=30°.
,∠A=30°.
①求BD和AD的长;
②求tanC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
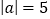 |,
|,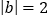 ,且
,且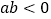 ,求
,求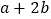 的值.
的值.解:(1)因为
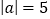 ,所以
,所以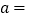 ______;
______;因为
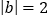 ,所以
,所以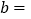 ______;
______;又因为
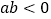 ,
,所以当
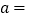 ______时,
______时,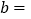 ______;
______;或当
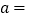 ______时,
______时,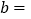 ______,
______,∴
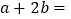 ______或_______.
______或_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】有4张写着以下数字的卡片,请按要求抽出卡片,完成下列各题:

(1)从中取出2张卡片,使这2张卡片上数字之积最大,最大值是________.
(2)从中取出2张卡片,使这2张卡片上数字之差最小,最小值是________.
(3)从中取出4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,请写出一种符合要求的运算式子________.(注:4个数字都必须用到且只能用一次.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A表示的有理数为﹣6,点B表示的有理数为6,点P从点A出发以每秒4个单位长度的速度在数轴上由A向B运动,当点P到达点B后立即返回,仍然以每秒4个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒).
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P沿数轴由点A到点B再回到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,请求出所有满足条件的t值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如下图1,2,他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )

A. 289 B. 1225 C. 1024 D. 1378
-
科目: 来源: 题型:
查看答案和解析>>【题目】按下面的程序计算:

若开始输入的x值为正整数,最后输出的结果为556,则开始输入的x值为____.
相关试题

