Question

【题目】在四边形OABC中，AB∥OC，BC⊥x轴于C，A（1，﹣1），B（3，﹣1），动点P从O点出发，沿x轴正方向以2个单位/秒的速度运动．过P作PQ⊥OA于Q．设P点运动的时间为t秒（0＜t＜2），△OPQ与四边形OABC重叠的面积为S．

（1）求经过O、A、B三点的抛物线的解析式并确定顶点M的坐标；
（2）用含t的代数式表示P、Q两点的坐标；
（3）将△OPQ绕P点逆时针旋转90°，是否存在t，使得△OPQ的顶点O或Q落在抛物线上？若存在，直接写出t的值；若不存在，请说明理由；
（4）求S与t的函数解析式．

Answer 1

【答案】
（1）

解：∵抛物线过点A（1，﹣1），B（3，﹣1），

∴抛物线的对称轴为直线x=2，

∴抛物线与x轴的另一个交点坐标为（4，0），

设抛物线的解析式为y=ax（x﹣4），

把A（1，﹣1）代入得a1（﹣3）=﹣1，解得a= ，

∴抛物线的解析式为y= x（x﹣4），即y= x2﹣ x；

∵y= （x﹣2）2﹣ ，

∴顶点M的坐标为（2，﹣ ）；

（2）

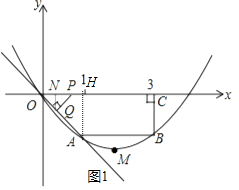
解：作QN⊥x轴于N，AH⊥x轴于H，如图1，

∵A（﹣1，1），

∴OH=AH=1，

∴△AOH为等腰直角三角形，

∴△ONQ为等腰直角三角形，

∴QN=ON=NP= OP=t，

∴P（2t，0），Q（t，﹣t）；

（3）

解：存在．

△OPQ绕P点逆时针旋转90°得到△O′PQ′，如图2，作Q′K⊥x轴于K，

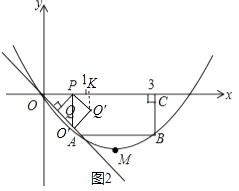
∠QPQ′=90°，PO′⊥x轴，PO′=PO=2t，PQ′=PQ= t，则O′（2t，﹣2t）；

∵∠KPQ′=90°﹣∠OPQ=45°，

∵△PQ′K为等腰三角形，

∴PK=Q′k=t，

∴Q′（3t，﹣t），

当O′（2t，﹣2t）落在抛物线上时，﹣2t= 4t2﹣ 2t，解得t1=0，t2= ；

当Q′（3t，﹣t）落在抛物线上时，﹣t= 9t2﹣ 3t，解得t1=0，t2=1；

综上所述，当t为 或1时，使得△OPQ的顶点O或Q落在抛物线上；

（4）

解：当0＜t≤1时，如图1，S= t2t=t；

当1＜t≤ 时，如图3，PQ交AB于E点，S=S△POQ﹣S△AEQ= t2t﹣ （t﹣1）

2（t﹣1）=2t﹣1；

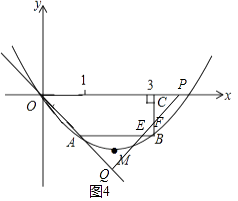
当 ＜t≤2，如图4，PQ交AB于E点，交BC于F点，

∵△POQ为等腰直角三角形，

∴∠CPF=45°，

∴△PCF为等腰直角三角形，

∴PC=CF=2t﹣3，

∴BF=1﹣（2t﹣3）=4﹣2t，

∴S△BEF= （4﹣2t）2=2t2﹣8t+8，

∴S=S梯形OABC﹣S△BEF= （2+3）1﹣（2t2﹣8t+8）=﹣2t2+8t﹣ ．

【解析】（1）利用对称性得到抛物线与x轴的另一个交点坐标为（4，0），则设交点式y=ax（x﹣4），然后把A点坐标代入求出a即可得到抛物线的解析式，再利用配方法得到顶点M的坐标；（2）作QN⊥x轴于N，AH⊥x轴于H，如图1，先判定△AOH和△ONQ为等腰直角三角形得到QN=ON=NP= OP=t，然后用t表示出P点和Q点坐标；（3）△OPQ绕P点逆时针旋转90°得到△O′PQ′，如图2，作Q′K⊥x轴于K，利用旋转的性质得∠QPQ′=90°，PO′⊥x轴，PO′=PO=2t，PQ′=PQ= t，再确定O′（2t，﹣2t），Q′（3t，﹣t），然后分别把O′（2t，﹣2t）或Q′（3t，﹣t）代入抛物线解析式可求出对应的t的值；（4）根据△OPQ与四边形OABC重叠部分的图形不同分类讨论：当0＜t≤1时，重叠部分为三角形，如图1，利用三角形面积公式表示出S；当1＜t≤ 时，如图3，PQ交AB于E点，重叠部分为梯形，利用三角形面积的差表示S；当 ＜t≤2，如图4，PQ交AB于E点，交BC于F点，重叠部分为梯形OABC减去△BEF，则利用梯形的面积减去三角形面积可表示出S．