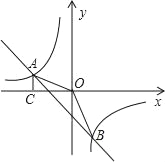
【题目】如图,一次函数y=kx﹣2的图象与反比例函数的图象交于A、B两点,过A作AC⊥x轴于点C.已知cos∠AOC=![]() ,OA=
,OA=![]() .
.
(1)求反比例函数及直线AB的解析式;
(2)求△AOB的面积.
参考答案:
【答案】(1)反比例函数的解析式为y=﹣![]() ,直线AB的解析式为y=﹣
,直线AB的解析式为y=﹣![]() x﹣2;(2)
x﹣2;(2)![]()
【解析】试题分析:(1)通过解直角三角形求出线段AC、OC的长度,从而得出点A的坐标,结合反比例函数图像上点的特点,可得出反比例函数解析式,由点A的坐标利用待定系数法即可求出直线AB的解析式;
(2)根据直线AB的解析式找出直线AB与x轴的交点坐标,再将一次函数解析式代入到反比例函数解析式中,解方程得出点B的坐标,分割三角形AOB,利用三角形的面积公式以及A、B的坐标即可得出结论.
试题解析:(1)∵AC⊥x轴,![]() ,
,
∴![]() ,
,
解得CO=2,
∴AC=![]() =1,
=1,
∴点A的坐标为(﹣2,1),
设反比例函数解析式为y=![]() ,则a=﹣2×1=﹣2,
,则a=﹣2×1=﹣2,
∴反比例函数的解析式为y=﹣![]() .
.
将点A(﹣2,1)代入到y=kx﹣1中,可得
1=﹣2k﹣2,
解得:k=﹣![]() ,
,
∴直线AB的解析式为y=﹣![]() x﹣2.
x﹣2.
(2)令一次函数y=﹣![]() x﹣2=0,
x﹣2=0,
解得:x=﹣![]() ,
,
即一次函数图象与x轴交于(﹣![]() ,0).
,0).
将y=﹣![]() x﹣2代入到反比例函数y=﹣
x﹣2代入到反比例函数y=﹣![]() 中,可得
中,可得
﹣![]() x﹣2=﹣
x﹣2=﹣![]() ,
,
即3x2+4x﹣4=0,
解得:x1=﹣2,x2=![]() .
.
∵y=﹣![]() x﹣2中,当x=
x﹣2中,当x=![]() 时,y=﹣3.
时,y=﹣3.
∴B(![]() ,﹣3).
,﹣3).
∴S△AOB=![]() ×
×![]() ×[1﹣(﹣3)]=
×[1﹣(﹣3)]=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我校4月份举办了教职工羽毛球赛,本次比赛共分三个项目:男双、女双和混双.比赛规定参赛男教师只能在男双或混双中选报一项,参赛女教师只能在女双或混双中选报一项,现将参赛人数和各项的参赛队数(两人组成一队)绘制成了如下不完整的统计图:
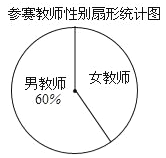
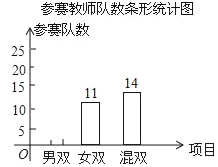
(1)本次比赛共有_____名参赛教师,并补全条形统计图;
(2)已知男双冠军分别是音乐教师和体育教师,女双冠军都是数学教师,混双冠军分别是数学男教师和美术女教师.暑假期问市教委将举办全市中小学教师羽毛球比赛,比赛规定:每所学校的参赛人数为两人,且参赛教师不得属于同一学科.所以学校决定:从三支冠军队伍中的数学教师中随机选取一人,再从其他教师中选取一人参加比赛.请用列表法或画树状图的方法求出所选两位教师恰好搭档参加混双项目的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若AC=8cm,CB=6cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a,其它条件不变,你能猜想MN的长度吗?写出你的结论并说明理由;
(3)若点C在线段AB的延长线上,且满足AC-BC=b,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形并写出你的结论(不必说明理由).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只甲虫在 5×5 的方格(每小格边长为 1)上沿着网格线运动.它从 A处出发去看望 B、C、D 处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从 A 到 B 记为:A→B(+1,+4),从 B 到 A 记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C( , ),B→C( , ),C→D ( , );
(2)若这只甲虫的行走路线为 A→B→C→D,请计算该甲虫走过的最少路程;
(3)若这只甲虫从 A 处去甲虫 P 处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出 P 的位置.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图

如图1,四边形ABCD和四边形BCMD都是菱形,
(1)求证:∠M=60°
(2)如图2,点E在边AD上,点F在边CM上,连接EF交CD于点H,若AE=MF,求证:EH=HF;
(3)如图3,在第(2)小题的条件下,连接BH,若EF⊥CM,AB=3,求BH的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AE=ED=2,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:我们把对角线相等的四边形叫做和美四边形.
 请举出一种你所学过的特殊四边形中是和美四边形的例子.
请举出一种你所学过的特殊四边形中是和美四边形的例子. 如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形; 如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,
如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O, ,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
相关试题

