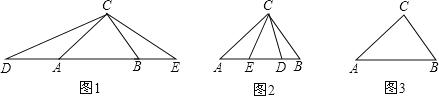
【题目】(1)如图(1),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在线段BA、AB的延长线上,且AD=AC,BE=BC,则∠DCE= ;
(2)如图(2),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
(3)在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在直线AB上,且AD=AC,BE=BC,则∠求DCE的度数(直接写出答案);
(4)如图(3),在△ABC中,AB=14,AC=15,BC=13,点D、E在直线AB上,且AD=AC,BE=BC.请根据题意把图形补画完整,并在图形的下方直接写出△DCE的面积.(如果有多种情况,图形不够用请自己画出,各种情况用一个图形单独表示).
参考答案:
【答案】(1)130°.(2)50°;(3)40°;(4)72.见解析
【解析】
试题分析:(1)根据等腰三角形的性质得到∠ACD=∠D,∠BCE=∠E,由三角形的内角和得到∠CAB+∠CBA=100°,根据三角形的外角的性质得到∠CDA+∠BCE=![]() (∠CAB+∠CBA)=50°,即可得到结论;
(∠CAB+∠CBA)=50°,即可得到结论;
(2)根据三角形的内角和和外角的性质即可得到结论;
(3)点D、E分别在直线AB上,除去(1)(2)两种情况,还有两种情况,如图3,由(1)知,∠D=![]() CAB,由(2)知∠CEB=
CAB,由(2)知∠CEB=![]() ,列方程即可求得结果.
,列方程即可求得结果.
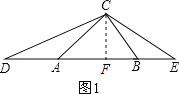
(4)在△ABC中,AB=14,AC=15,BC=13,过C作CF⊥AB与F,根据勾股定理求得AB边上的高CF=12,然后根据三角形的面积公式即可强大的结论.
解:(1)∵AD=AC,BE=BC,
∴∠ACD=∠D,∠BCE=∠E,
∵∠ACB=80°,
∴∠CAB+∠CBA=100°,
∴∠CDA+∠BCE=![]() (∠CAB+∠CBA)=50°,
(∠CAB+∠CBA)=50°,
∴∠DCE=130°,
故答案为:130°.
(2)∵∠ACB=80°,
∴∠A+∠B=100°,
∵AD=AC,BE=BC,
∴∠ACD=∠ADC,∠BEC=∠BCE,
∴∠ADC=![]() ,∠BEC=
,∠BEC=![]() ,
,
∴∠ADC+∠BEC=180°﹣![]() (∠A+∠B)=130°,
(∠A+∠B)=130°,
∴∠DCE=50°;
(3)点D、E分别在直线AB上,除去(1)(2)两种情况,还有两种情况,如图3,
由(1)知,∠D=![]() CAB,由(2)知∠CEB=
CAB,由(2)知∠CEB=![]() ,
,
∴∠CEB=∠D+∠DCE,
∴![]() =
=![]() CAB+∠DCE,
CAB+∠DCE,
∴∠DCE=40°,
如图4,同理∠DCE=40°;
(4)在△ABC中,AB=14,AC=15,BC=13,
过C作CF⊥AB与F,
则AC2﹣AF2=BC2﹣BF2,即152﹣AF2=132﹣(14﹣AF)2,
解得:AF=9,
∴CF=12,
①如图1,DE=AB+AC+BC=42,
∴S△CDE=![]() ×42×12=252;
×42×12=252;
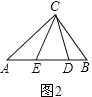
②如图2,DE=AC+BC﹣AB=14,
∴S△CDE=![]() ×14×12=84;
×14×12=84;
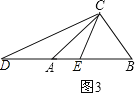
③如图3,DE=AC+AB﹣BC=16,
∴S△CDE=![]() ×16×12=96;
×16×12=96;
④如图4,DE=AB+BC﹣AC=12,
∴S△CDE=![]() ×12×12=72.
×12×12=72.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两地相距900千米,一列快车从甲地出发匀速开往乙地,速度为120千米/时;快车开出30分钟时,一列慢车从乙地出发匀速开往甲地,速度为90千米/时.设慢车行驶的时间为x小时,快车到达乙地后停止行驶,根据题意解答下列问题:
(1)当快车与慢车相遇时,求慢车行驶的时间;
(2)请从下列(A),(B)两题中任选一题作答.
我选择: .
(A)当两车之间的距离为315千米时,求快车所行的路程;
(B)①在慢车从乙地开往甲地的过程中,求快慢两车之间的距离;(用含x的代数式表示)
②若第二列快车也从甲地出发匀速驶往乙地,速度与第一列快车相同,在第一列快车与慢车相遇后30分钟时,第二列快车与慢车相遇,直接写出第二列快车比第一列快车晚出发多少小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区环保部门为了提高宣传垃圾分类的实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,进行整理后,绘制了如下两幅不完整的统计图:

根据统计图解答下列问题:
(1)求抽样调查的生活垃圾的总吨数以及其中的有害垃圾的吨数;
(2)求扇形统计图中,“D”部分所对应的圆心角的度数,并将条形统计图补充完整;
(3)调查发现,在可回收物中废纸垃圾约占
 ,每回收1吨废纸可再造0.85吨的再生纸,假设该城市每月生产的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可制成再生纸多少吨?
,每回收1吨废纸可再造0.85吨的再生纸,假设该城市每月生产的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可制成再生纸多少吨? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且DA=DC,链接AC,AD,延长AD交BM地点E.
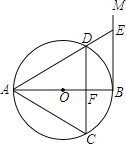
(1)求证:△ACD是等边三角形.
(2)连接OE,若DE=2,求OE的长.
-
科目: 来源: 题型:
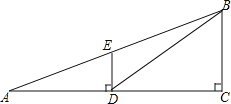
查看答案和解析>>【题目】如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设
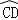 、
、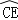 的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .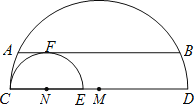
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,已知∠A=35°,则锐角∠C=________.
相关试题

