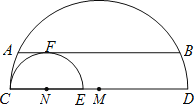
【题目】如图,直径分别为CD、CE的两个半圆相切于点C,大半圆M的弦与小半圆N相切于点F,且AB∥CD,AB=4,设![]() 、
、![]() 的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
的长分别为x、y,线段ED的长为z,则z(x+y)的值为 .
参考答案:
【答案】8π.
【解析】
试题分析:过M作MG⊥AB于G,连MB,NF,根据垂径定理得到BG=AG=2,利用勾股定理可得MB2﹣MG2=22=4,再根据切线的性质有NF⊥AB,而AB∥CD,得到MG=NF,设⊙M,⊙N的半径分别为R,r,则z(x+y)=(CD﹣CE)(πR+πr)=(R2﹣r2)2π,即可得到z(x+y)的值.
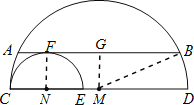
解:过M作MG⊥AB于G,连MB,NF,如图,
而AB=4,
∴BG=AG=2,
∴MB2﹣MG2=22=4,
又∵大半圆M的弦与小半圆N相切于点F,
∴NF⊥AB,
∵AB∥CD,
∴MG=NF,
设⊙M,⊙N的半径分别为R,r,
∴z(x+y)=(CD﹣CE)(πR+πr),
=(2R﹣2r)(R+r)π,
=(R2﹣r2)2π,
=42π,
=8π.
故答案为:8π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且DA=DC,链接AC,AD,延长AD交BM地点E.
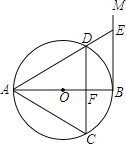
(1)求证:△ACD是等边三角形.
(2)连接OE,若DE=2,求OE的长.
-
科目: 来源: 题型:
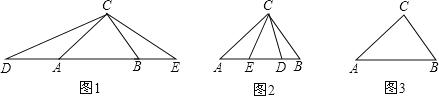
查看答案和解析>>【题目】(1)如图(1),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在线段BA、AB的延长线上,且AD=AC,BE=BC,则∠DCE= ;
(2)如图(2),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
(3)在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在直线AB上,且AD=AC,BE=BC,则∠求DCE的度数(直接写出答案);
(4)如图(3),在△ABC中,AB=14,AC=15,BC=13,点D、E在直线AB上,且AD=AC,BE=BC.请根据题意把图形补画完整,并在图形的下方直接写出△DCE的面积.(如果有多种情况,图形不够用请自己画出,各种情况用一个图形单独表示).
-
科目: 来源: 题型:
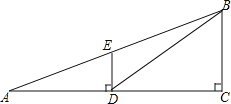
查看答案和解析>>【题目】如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,已知∠A=35°,则锐角∠C=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】6﹣(+3)﹣(﹣4)+(﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年春节期间,在网络上用“百度”搜索引擎搜索“开放二孩”,能搜索到与之相关的结果个数约为45100000,这个数用科学记数法表示为 .
相关试题

