【题目】如图,在ABCD中,对角线AC与BD交于点O,若增加一个条件,使ABCD成为菱形,下列给出的条件不正确的是( ) 
A.AB=AD
B.AC⊥BD
C.AC=BD
D.∠BAC=∠DAC
参考答案:
【答案】C
【解析】解:A、根据菱形的定义可得,当AB=AD时ABCD是菱形;
B、根据对角线互相垂直的平行四边形是菱形即可判断,ABCD是菱形;
C、对角线相等的平行四边形是矩形,不一定是菱形,命题错误;
D、∠BAC=∠DAC时,
∵ABCD中,AD∥BC,
∴∠ACB=∠DAC,
∴∠BAC=∠ACB,
∴AB=AC,
∴ABCD是菱形.
∴∠BAC=∠DAC.故命题正确.
故选C.
根据菱形的定义和判定定理即可作出判断.本题考查了菱形的判定定理,正确记忆定义和判定定理是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD的两个顶点A、C在反比例函数y=
 (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点 
(1)已知点A的坐标是(2,3),求k的值及C点的坐标;
(2)若△APO的面积为2,求点D到直线AC的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形

(1)求证:△DFB是等腰三角形;
(2)若DA= AF,求证:CF⊥AB.
AF,求证:CF⊥AB. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣(2k+1)x+k2+k(k>0)
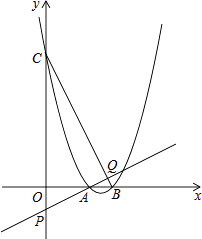
(1)当k= 时,求这个二次函数的顶点坐标;
时,求这个二次函数的顶点坐标;
(2)求证:关于x的一元次方程x2﹣(2k+1)x+k2+k=0有两个不相等的实数根;
(3)如图,该二次函数与x轴交于A、B两点(A点在B点的左侧),与y轴交于C点,P是y轴负半轴上一点,且OP=1,直线AP交BC于点Q,求证: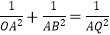 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( )
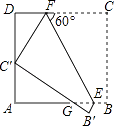
A.3 ﹣4
﹣4
B.4 ﹣5
﹣5
C.4﹣2
D.5﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=3,连接AC,⊙P和⊙Q分别是△ABC和△ADC的内切圆,则PQ的长是( )

A.
B.
C.
D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC⊥BC,AC=BC,D是BC上一点,连接AD,与∠ACB的平分线交于点E,连接BE.若S△ACE=
 ,S△BDE=
,S△BDE=  ,则AC= .
,则AC= . 
相关试题

