Question

【题目】问题背景：如图①，在四边形ADBC中，∠ACB＝∠ADB＝90°，AD＝BD，探究线段AC、BC、CD之间的数量关系.

小吴同学探究此问题的思路是：将ΔBCD绕点D逆时针旋转90°到ΔAED处，点B、C分别落在点A、E处（如图②），易证点C、A、E在同一条直线上，并且ΔCDE是等腰直角三角形，所以CE＝CD，从而得出结论：AC+BC＝CD.

　 图①　　　 　　图②　　　　　　　 图③ 图④

简单应用：

（1）在图①中，若AC＝，BC＝2，则CD＝ .

（2）如图③，AB是⊙O的直径，点C、D在⊙O上，弧AD＝弧BD，若AB＝13，BC＝12，求CD的长.

拓展延伸：

（3）如图④，∠ACB＝∠ADB＝90°，AD＝BD，若AC＝m，BC＝n（m<n），求CD的长（用含m，n的代数式表示）.

Answer 1

【答案】(1) 3； (2)CD= ； (3) CD=.

【解析】试题分析：（1）由题意可知：AC+BC=CD，所以将AC与BC的长度代入即可得出CD的长度；

（2）连接AC、BD、AD即可将问题转化为第（1）问的问题，利用题目所给出的证明思路即可求出CD的长度；

（3）以AB为直径作⊙O，连接OD并延长交⊙O于点D1，由（2）问题可知：AC+BC=CD1；又因为CD1=D1D，所以利用勾股定理即可求出CD的长度.

试题解析：(1)由题意知：AC+BC=CD，∴+2=CD， ∴CD=3；

(2)如图3，连接AC、BD、AD，

∵AB是⊙O的直径，∴∠ADB=∠ACB=90，

∵AD=BD，∴AD=BD，

∵AB=13，BC=12，∴由勾股定理得：AC=5，

由图1得：AC+BC=CD，5+12=CD，∴CD= .

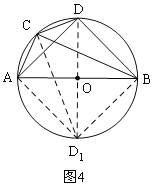
(3)解法一：以AB为直径作⊙O,连接DO并延长交⊙O于点D1，

连接D1A、D1B、D1C、CD,如图4,

由(2)得：AC+BC=D1C，∴D1C=2，

∵D1D是⊙O的直径，∴∠D1CD=90，

∵AC=m，BC=n，∴由勾股定理可求得：AB2=m2+n2，∴D1D2=AB2=m2+n2，

∵D1C2+DC2=D1D2，∴CD2=m2+n2=,

∵m<n，∴CD=；

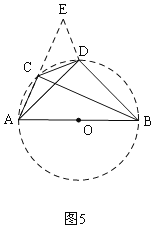
解法二：如图5,∵∠ACB=∠DB=90，

∴A、B. C.D在以AB为直径的圆上，∴∠DAC=∠DBC，

将△BCD绕点D,逆时针旋转90到△AED处，点B，C分别落在点A，E处，

∴△BCD≌△AED，∴CD=ED，∠ADC=∠ADE，

∴∠ADC∠ADC=∠ADE∠ADC，

即∠ADB=∠CDE=90，∴△CDE是等腰直角三角形,所以CE=CD，

∵AC=m，BC=n=AE，∴CE=nm，∴CD=.