【题目】如图所示,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2012m停下,则这个微型机器人停在( )

A.点A处 B.点B处 C.点C处 D.点E处
参考答案:
【答案】C
【解析】
试题分析:根据等边三角形和全等三角形的性质,可以推出,每行走一圈一共走了6个1m,2012÷6=335…2,行走了335圈又两米,即落到C点.
解:∵两个全等的等边三角形的边长为1m,
∴机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动一圈,即为6m,
∵2012÷6=335…2,即正好行走了335圈又两米,回到第三个点,
∴行走2012m停下,则这个微型机器人停在C点.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1的函数表达式为y1=﹣3x+3,且l1与x轴交于点D,直线l2:y2=kx+b经过点A,B,与直线l1交于点C.
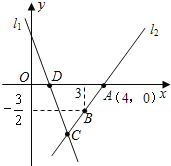
(1)求直线l2的函数表达式及C点坐标;
(2)求△ADC的面积;
(3)当x满足何值时,y1>y2;(直接写出结果)
(4)在直角坐标系中有点E,和A,C,D构成平行四边形,请直接写出E点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(-3,7)到y轴的距离为( )
A. -3 B. 3 C. 7 D. -7
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x﹣5)(2x﹣1)=3的根的判别式b2﹣4ac= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②2a+b=0;③当x≠1时,a+b>ax2+bx;④a﹣b+c>0.
其中正确的有 .
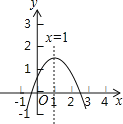
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2﹣5x=3,求(x﹣1)(2x﹣1)﹣(x+1)2+1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中正确的是( )
A.2x+3y=5xy B.a3﹣a2=a
C.(a﹣1)(a﹣2)=a2+a﹣2 D.(a﹣ab)÷a=1﹣b
相关试题

