【题目】如图,直线l1的函数表达式为y1=﹣3x+3,且l1与x轴交于点D,直线l2:y2=kx+b经过点A,B,与直线l1交于点C.
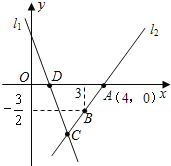
(1)求直线l2的函数表达式及C点坐标;
(2)求△ADC的面积;
(3)当x满足何值时,y1>y2;(直接写出结果)
(4)在直角坐标系中有点E,和A,C,D构成平行四边形,请直接写出E点的坐标.
参考答案:
【答案】(1)直线l2的解析式为y2=![]() x﹣6;点C的坐标为(2,﹣3);(2)
x﹣6;点C的坐标为(2,﹣3);(2)![]() ;(3)x<2;(4)E1(5,﹣3)、E2(3,3)、E3(﹣1,﹣3).
;(3)x<2;(4)E1(5,﹣3)、E2(3,3)、E3(﹣1,﹣3).
【解析】
试题分析:(1)利用待定系数法求出直线l2的解析式,利用二元一次方程组求出两条直线的交点C的坐标;
(2)根据坐标与图形图中求出点D的坐标,根据三角形的面积公式计算即可;
(3)运用数形结合思想解答;
(4)分以AC为对角线、以AD为对角线、以CD为对角线三种情况,根据平行四边形的性质解答即可.
解:(1)∵点A(4,0)、B(3,﹣![]() )在直线l2:y2=kx+b上,
)在直线l2:y2=kx+b上,
∴ ,
,
解得: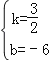 .
.
∴直线l2的解析式为y2=![]() x﹣6;
x﹣6;
由 ,
,
解得![]() .
.
∴点C的坐标为(2,﹣3);
(2)∵点D是直线l1:y=﹣3x+3与x轴的交点,
∴y=0时,0=﹣3x+3,解得x=1,
∴D(1,0),
∵A(4,0),
∴AD=4﹣1=3,
∴△ADC的面积=![]() ×3×3=
×3×3=![]() ;
;
(3)由图象可知,当x<2时,y1>y2;
(4)符合条件的E点的坐标为E1(5,﹣3)、E2(3,3)、E3(﹣1,﹣3),
①以AC为对角线时,
∵四边形ADCE是平行四边形,
∴CE∥DA,CE=DA=3,
∴将点C(2,﹣3)向右平移3个单位得到点E,即E1(5,﹣3);
②以AD为对角线时,
∵四边形ACDE是平行四边形,
∴CE与AD互相平分,即CE与AD的中点重合,则E2(3,3);
③以CD为对角线时,
∵四边形ADEC是平行四边形,
∴CE∥AD,CE=AD=3,
∴将点C(2,﹣3)向左平移3个单位得到点E,即E3(﹣1,﹣3);
综上所述,符合条件的E点的坐标为E1(5,﹣3)、E2(3,3)、E3(﹣1,﹣3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠D=50°,则下列结论:①∠AOE=65°;②OF平分∠BOD;③∠GOE=∠DOF;④∠GOE=25°。其中正确的是:( )
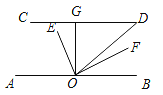
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=2x2向下平移1个单位,得到的抛物线是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题:
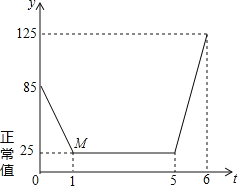
(1)写出题中的变量;
(2)写出点M的实际意义;
(3)求第1小时内,y与t的一次函数表达式;
(4)已知第5﹣6小时是小强妈妈做晚餐的时间,厨房内油烟导致PM2.5浓度升高.若该净化器吸收PM2.5的速度始终不变,则第6小时之后,预计经过多长时间室内PM2.5浓度可恢复正常?
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(-3,7)到y轴的距离为( )
A. -3 B. 3 C. 7 D. -7
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程(x﹣5)(2x﹣1)=3的根的判别式b2﹣4ac= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2012m停下,则这个微型机器人停在( )

A.点A处 B.点B处 C.点C处 D.点E处
相关试题

