【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A. abc<0 B. -3a+c<0
C. b2-4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c
参考答案:
【答案】B
【解析】解:A.由开口向下,可得a<0;又由抛物线与y轴交于负半轴,可得c<0,然后由对称轴在y轴右侧,得到b与a异号,则可得b>0,故得abc>0,故本选项错误;
B.根据图知对称轴为直线x=2,即![]() =2,得b=﹣4a,再根据图象知当x=1时,y=a+b+c=a﹣4a+c=﹣3a+c<0,故本选项正确;
=2,得b=﹣4a,再根据图象知当x=1时,y=a+b+c=a﹣4a+c=﹣3a+c<0,故本选项正确;
C.由抛物线与x轴有两个交点,可得b2﹣4ac>0,故本选项错误;
D.y=ax2+bx+c= ![]() ,∵
,∵![]() =2,∴原式=
=2,∴原式= ![]() ,∴向左平移2个单位后所得到抛物线的解析式为
,∴向左平移2个单位后所得到抛物线的解析式为![]() ,故本选项错误;
,故本选项错误;
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,正方形
 的两边分别在正方形
的两边分别在正方形 的边
的边 和
和 上,连接
上,连接 .填空:线段
.填空:线段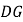 与
与 的数量关系为________;直线
的数量关系为________;直线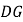 与
与 所夹锐角的大小为________.
所夹锐角的大小为________.


(2)如图②,将正方形
 绕点
绕点 顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.(3)把图②中的正方形都换成菱形,且
 ,如图③,直接写出
,如图③,直接写出 ______.
______. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:基本不等式
 ≤
≤ (a>0,b>0),当且仅当a=b时,等号成立.其中我们把
(a>0,b>0),当且仅当a=b时,等号成立.其中我们把 叫做正数a、b的算术平均数,
叫做正数a、b的算术平均数, 叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.例如:在x>0的条件下,当x为何值时,x+
 有最小值,最小值是多少?
有最小值,最小值是多少?解:∵x>0,
 >0∴
>0∴ ≥
≥ 即是x+
即是x+ ≥2
≥2
∴x+
 ≥2
≥2当且仅当x=
 即x=1时,x+
即x=1时,x+ 有最小值,最小值为2.
有最小值,最小值为2.请根据阅读材料解答下列问题
(1)若x>0,函数y=2x+
 ,当x为何值时,函数有最小值,并求出其最小值.
,当x为何值时,函数有最小值,并求出其最小值.(2)当x>0时,式子x2+1+
 ≥2成立吗?请说明理由.
≥2成立吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表给出了代数式﹣x2+bx+c与x的一些对应值:
x
…
﹣2
﹣1
0
1
2
3
…
﹣x2+bx+c
…
5
n
c
2
﹣3
﹣10
…
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=﹣x2+bx+c,直接写出0≤x≤2时y的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形
 中,
中, ,
, ,动点
,动点 从
从 出发,以每秒1个单位的速度沿射线
出发,以每秒1个单位的速度沿射线 方向移动,作
方向移动,作 关于直线
关于直线 的对称
的对称 ,设点
,设点 的运动时间为
的运动时间为 .
.

(1)当
 时.
时.①如图2.当点
 落在
落在 上时,显然
上时,显然 是直角三角形,求此时
是直角三角形,求此时 的值;
的值;②当点
 不落在
不落在 上时,请直接写出
上时,请直接写出 是直角三角形时
是直角三角形时 的值;
的值;(2)若直线
 与直线
与直线 相交于点
相交于点 ,且当
,且当 时,
时, .问:当
.问:当 ,
, 的大小是否发生变化,若不变,请说明理由.
的大小是否发生变化,若不变,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是弧EB的中点,则下列结论:
①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
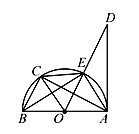
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

