【题目】如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE. 
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.
参考答案:
【答案】
(1)证明:∵将△ABD绕点A逆时针旋转60°得△ACE
∴△ABD≌△ACE,∠BAC=∠DAE,
∴AD=AE,BD=CE,∠AEC=∠ADB=120°,
∵△ABC为等边三角形
∴∠BAC=60°
∴∠DAE=60°
∴△ADE为等边三角形,
∴AD=DE
(2)∠ADC=90°,∠AEC=120°,∠DAE=60°
∴∠DCE=360°﹣∠ADC﹣∠AEC﹣∠DAE=90°
(3)∵△ADE为等边三角形
∴∠ADE=60°
∴∠CDE=∠ADC﹣∠ADE=30°
又∵∠DCE=90°
∴DE=2CE=2BD=2,
∴AD=DE=2
在Rt△DCE中, ![]()
【解析】(1)利用旋转的性质和等边三角形的性质先判断出△ADE是等边三角形即可;(2)利用四边形的内角和即可求出结论;(3)先求出CD,再用勾股定理即可求出结论.
【考点精析】利用等腰三角形的性质和等边三角形的性质对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);等边三角形的三个角都相等并且每个角都是60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC,BD交于点E,DF⊥AC于F点,若∠ADF=3∠FDC,则∠DEC的度数是( )
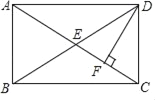
A. 30° B. 45° C. 50° D. 55°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=6,∠A=135°,点P是菱形内部一点,且满足S△PCD=
 ,则PC+PD的最小值是_____.
,则PC+PD的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C为⊙O上的一点,点D是
 的中点,过D作⊙O的切线交AC于E,DE=3,CE=1.
的中点,过D作⊙O的切线交AC于E,DE=3,CE=1. 
(1)求证:DE⊥AC;
(2)求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=(x﹣1)2+n与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3),点D与点C关于抛物线的对称轴对称.
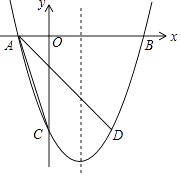
(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线对称轴上的一动点,当△PAC的周长最小时,求出点P的坐标;
(3)点Q在x轴上,且∠ADQ=∠DAC,请直接写出点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
 ,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( )
,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( ) 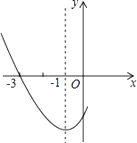
A.①②
B.②③
C.①②④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】一圆的半径是10cm,圆内的两条平行弦长分别为12cm和16cm,则这两条平行弦之间的距离为 .
相关试题

