【题目】如图,AB为⊙O的直径,点C为⊙O上的一点,点D是 ![]() 的中点,过D作⊙O的切线交AC于E,DE=3,CE=1.
的中点,过D作⊙O的切线交AC于E,DE=3,CE=1. 
(1)求证:DE⊥AC;
(2)求⊙O的半径.
参考答案:
【答案】
(1)证明:连接AD,
∵DE是⊙O的切线,
∴∠ODE=90°,
∵D是 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴∠CAD=∠OAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠CAD=∠ODA,
∴AE∥OD,
∴∠AED=180°﹣∠ODE=90°,
∴DE⊥AC
(2)解:作OF⊥AC于F,
则AF=CF,四边形OFED是矩形,
∴OF=ED=3,OD=EF,
设⊙O的半径为R,则AF=CF=R﹣1,
在Rt△AOF中,AF2+OF2=OA2,
∴(R﹣1)2+32=R2,
解得R=5,
即⊙O的半径为5.

【解析】(1)连接AD,由DE是⊙O的切线,得到∠ODE=90°,根据等腰三角形的性质得到∠ODA=∠OAD,等量代换得到∠CAD=∠ODA,根据平行线的判定 定理得到AE∥OD,于是得到结论;(2)作OF⊥AC于F,推出四边形OFED是矩形,根据矩形的性质得到OF=ED=3,OD=EF,设⊙O的半径为R,则AF=CF=R﹣1,根据勾股定理列方程即可得到结论.
【考点精析】本题主要考查了圆心角、弧、弦的关系和切线的性质定理的相关知识点,需要掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是_____度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在_____等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC,BD交于点E,DF⊥AC于F点,若∠ADF=3∠FDC,则∠DEC的度数是( )
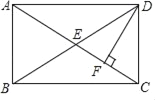
A. 30° B. 45° C. 50° D. 55°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=6,∠A=135°,点P是菱形内部一点,且满足S△PCD=
 ,则PC+PD的最小值是_____.
,则PC+PD的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.

(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=(x﹣1)2+n与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3),点D与点C关于抛物线的对称轴对称.
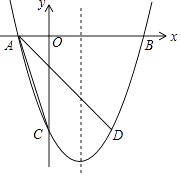
(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线对称轴上的一动点,当△PAC的周长最小时,求出点P的坐标;
(3)点Q在x轴上,且∠ADQ=∠DAC,请直接写出点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
 ,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( )
,y2)是抛物线上两点,则y1<y2 , 其中说法正确的是( ) 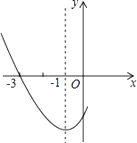
A.①②
B.②③
C.①②④
D.②③④
相关试题

