Question

【题目】某兴趣小组开展课外活动．如图，A，B两地相距12米，小明从点A出发沿AB方向匀速前进，2秒后到达点D，此时他（CD）在某一灯光下的影长为AD，继续按原速行走2秒到达点F，此时他在同一灯光下的影子仍落在其身后，并测得这个影长为1.2米，然后他将速度提高到原来的1.5倍，再行走2秒到达点H，此时他（GH）在同一灯光下的影长为BH（点C，E，G在一条直线上）．

（1）请在图中画出光源O点的位置，并画出他位于点F时在这个灯光下的影长FM（不写画法）
（2）求小明原来的速度。

Answer 1

【答案】
（1）

解：如图，

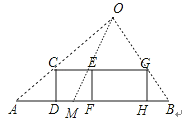
（2）

解：设小明原来的速度为xm/s，则CE=2xm，AM=AF﹣MF=（4x﹣1.2）m，EG=2×1.5x=3xm，BM=AB﹣AM=12﹣（4x﹣1.2）=13.2﹣4x，

∵点C，E，G在一条直线上，CG∥AB，

∴△OCE∽△OAM，△OEG∽△OMB，

∴=，=，

∴=，即=，

解得x=1.5，经检验x=1.5为方程的解，

∴小明原来的速度为1.5m/s．

答：小明原来的速度为1.5m/s．

【解析】（1）利用中心投影的定义画图；
（2）设小明原来的速度为xm/s，则CE=2xm，AM=AF﹣MF=（4x﹣1.2）m，EG=2×1.5x=3xm，BM=AB﹣AM=12﹣（4x﹣1.2）=13.2﹣4x，根据相似三角形的判定方法得到△OCE∽△OAM，△OEG∽△OMB，列出方程求解即可
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识，掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解，以及对中心投影的理解，了解手电筒、路灯和台灯的光线可以看成是从一个点发出的，这样的光线所形成的投影称为中心投影；作一物体中心投影的方法：过投影中心与物体顶端作直线，直线与投影面的交点与物体的底端之间的线段即为物体的影子．