【题目】如图,已知E、F分别为平行四边形ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,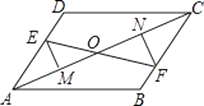
求证:
(1)EM=FN;
(2)EF与MN互相平分.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,
∴∠EAM=∠FCN,
∵DE=BF,
∴AE=CF,∵EM⊥AC于M,FN⊥AC于N,∴∠AME=∠CNF=90°,
在△AEM和△CFN中,  ,
,
∴△AEM≌△CFN(AAS),
∴EM=FN
(2)证明:连接EN、FM,如图所示: 
∵EM⊥AC,FN⊥AC,
∴∠AME=∠EMN=∠FNC=∠FNM=90°,
∴EM∥FN,
又∵由(1)得EM=FN,
∴四边形EMFN是平行四边形,
∴EF与MN互相平分.
【解析】(1)根据平行四边形的性质得出AD∥BC,AD=BC,,进而得出∠EAM=∠FCN,根据等式的性质及垂直的定义知AE=CF,∠AME=∠CNF=90°,用AAS判断出△AEM≌△CFN,根据三角形全等的性质得出结论;
(2)连接EN、FM根据垂直于同一直线的两条直线互相平行得出EM∥FN,又EM=FN,利用平行四边形的判定方法判断出四边形EMFN是平行四边形,根据平行四边形的性质得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班50名学生的处理方式进行统计,得出相关统计表和统计图:

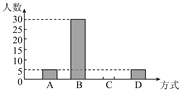
请根据图表所提供的信息回答下列问题:
(1)统计表中的m=_____,n=_____;
(2)补全频数分布直方图;
(3)若该校有2000名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
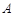 、
、 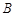 均在边长为1的正方形网格格点上.
均在边长为1的正方形网格格点上.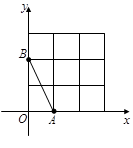
(1)在网格的格点中,找一点C,使△ABC是直角三角形,且三边长均为无理数(只画出一个,并涂上阴影);
(2)若点P在图中所给网格中的格点上,△APB是等腰三角形,满足条件的点P共有个;
(3)若将线段AB绕点A顺时针旋转90°,写出旋转后点B的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块四边形草地ABCD,其中∠B=90°,AB=4m,BC=3m , AD=12m, CD =13cm,求这块草地的面积.
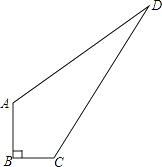
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形中有一个内角为40°,则其底角的度数是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决“最后一公里一的交通接驳同题,苏州市投放了大量公租自行车供 市民使用到2014年底,全市已有公租自行车25 000辆,租赁点600个,预计到2016年底,全市将有公租自行车50 000辆,并且平均每个租赁点的公租自行车数量是2014年底平均每个租赁点的公租自行车数量的1.2倍,预计到2016年底,全市将有租赁点多少个?
相关试题

