【题目】某班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班50名学生的处理方式进行统计,得出相关统计表和统计图:

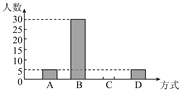
请根据图表所提供的信息回答下列问题:
(1)统计表中的m=_____,n=_____;
(2)补全频数分布直方图;
(3)若该校有2000名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?
参考答案:
【答案】(1) 5,10;(2) 补图见解析;(3) 1200人.
【解析】试题分析:(1)根据条形统计图可以求得m的值,然后利用50减去其它各组的人数即可求得n的值;
(2)根据(1)的结果即可作出统计图;
(3)利用总人数2000乘以所占的比例即可求解.
试题解析:(1)根据条形图可以得到:m=5,n=50-5-30-5=10(人)
故答案是:5,10;
(2)如图,
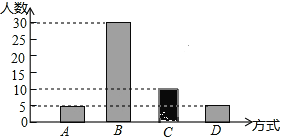 ;
;
(3)2000×![]() =1200(人).
=1200(人).
-
科目: 来源: 题型:
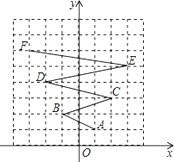
查看答案和解析>>【题目】如图,在平面直角坐标系中,一个点从A(a1 , a2)出发沿图中路线依次经过B(a3 , a4),C(a5 , a6),D(a7 , a8),…,按此一直运动下去,则a2015+a2016的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
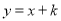 和双曲线
和双曲线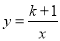 (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1,当k=2时,△OAB的面积记为S2,…,依此类推,当k=n时,△OAB的面积记为Sn,若S1+S2+…+Sn=
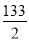 ,求n的值.
,求n的值.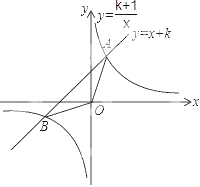
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
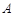 、
、  均在边长为1的正方形网格格点上.
均在边长为1的正方形网格格点上.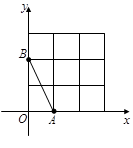
(1)在网格的格点中,找一点C,使△ABC是直角三角形,且三边长均为无理数(只画出一个,并涂上阴影);
(2)若点P在图中所给网格中的格点上,△APB是等腰三角形,满足条件的点P共有个;
(3)若将线段AB绕点A顺时针旋转90°,写出旋转后点B的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块四边形草地ABCD,其中∠B=90°,AB=4m,BC=3m , AD=12m, CD =13cm,求这块草地的面积.
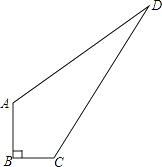
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F分别为平行四边形ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,
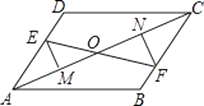
求证:
(1)EM=FN;
(2)EF与MN互相平分.
相关试题

