搜索
【题目】如图，∠AOB=90°，OA=90cm，OB=30cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少?
参考答案：
【答案】解：∵小球滚动的速度与机器人行走的速度相等 ∴BC=AC
设BC=AC=xcm ∴OC=（90－x）cm 在Rt△BOC中， 
∴ 
解得：x=50
答：机器人行走的路程BC为50cm
【解析】根据小球滚动的速度与机器人行走的速度相等 知BC=AC，设BC=AC=xcm ∴OC=（90－x）cm 在Rt△BOC中利用勾股定理列出方程求解即可。
【考点精析】掌握勾股定理的概念是解答本题的根本，需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，
、 
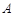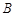均在边长为1的正方形网格格点上．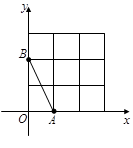
（1）在网格的格点中，找一点C，使△ABC是直角三角形，且三边长均为无理数（只画出一个，并涂上阴影）；
（2）若点P在图中所给网格中的格点上，△APB是等腰三角形，满足条件的点P共有个；
（3）若将线段AB绕点A顺时针旋转90°，写出旋转后点B的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一块四边形草地ABCD，其中∠B＝90°，AB＝4m，BC＝3m ， AD＝12m， CD =13cm，求这块草地的面积．
-
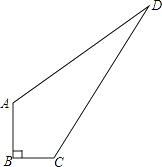
科目： 来源： 题型：
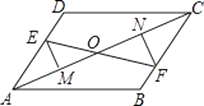
查看答案和解析>>【题目】如图，已知E、F分别为平行四边形ABCD的对边AD、BC上的点，且DE=BF，EM⊥AC于M，FN⊥AC于N，EF交AC于点O，
求证：
（1）EM=FN；
（2）EF与MN互相平分． -
科目： 来源： 题型：
查看答案和解析>>【题目】等腰三角形中有一个内角为40°，则其底角的度数是_____________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为解决“最后一公里一的交通接驳同题，苏州市投放了大量公租自行车供 市民使用到2014年底，全市已有公租自行车25 000辆，租赁点600个，预计到2016年底，全市将有公租自行车50 000辆，并且平均每个租赁点的公租自行车数量是2014年底平均每个租赁点的公租自行车数量的1.2倍，预计到2016年底，全市将有租赁点多少个？
-
科目： 来源： 题型：
查看答案和解析>>【题目】近年来，我国多个城市遭遇雾霾天气，空气中可吸入颗粒（又称PM2．5）浓度升高，为应对空气污染，小强家购买了空气净化器，该装置可随时显示室内PM2．5的浓度，并在PM2．5浓度超过正常值25（mg/m3）时吸收PM2．5以净化空气．随着空气变化的图象（如图），请根据图象，解答下列问题：
（1）写出点M的实际意义；
（2）求第1小时内，y与t的一次函数表达式；
（3）已知第5﹣6小时是小强妈妈做晚餐的时间，厨房内油烟导致PM2．5浓度升高．若该净化器吸收PM2．5的速度始终不变，则第6小时之后，预计经过多长时间室内PM2．5浓度可恢复正常？
相关试题
