搜索
【题目】如图，已知正三角形ABC的边长为1，E，F，G分别是AB，BC，CA上的点，且AE=BF=CG，设△EFG的面积为y，AE的长为x，则y关于x的函数的图象大致是（ ）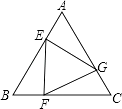
A.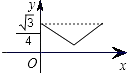
B.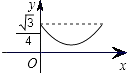
C.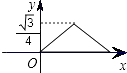
D.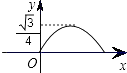
参考答案：
【答案】B
【解析】解：根据题意，有AE=BF=CG，且正三角形ABC的边长为1，
故BE=CF=AG=1﹣x；
故△AEG、△BEF、△CFG三个三角形全等．
在△AEG中，AE=x，AG=1﹣x，
则S△AEG= 
AE×AG×sinA= 
x（1﹣x）；
故y=S△ABC﹣3S△AEG= ﹣3× x（1﹣x）= （3x2﹣3x+1）．
故可得其图象为二次函数，且开口向上；
所以答案是：B．
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识，掌握等边三角形的三个角都相等并且每个角都是60°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】近年来，“在初中数学教学时总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注，为此，某校随机调查了n名学生对此问题的看法（看法分为三种：没有影响，影响不大，影响很大），并将调查结果 绘制成如下不完整的统计表和扇形统计图，根据统计图表提供的信息，解答下列问题：
n名学生对使用计算器影响计算能力的发展看法人数统计表看法
没有影响
影响不大
影响很大
学生人数（人）
40
60
m
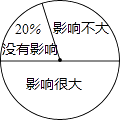
（1）求n的值；
（2）统计表中的m=；
（3）估计该校1800名学生中认为“影响很大”的学生人数． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图△ABC三个顶点的坐标分别为A（0，﹣3）、B（3，﹣2）、C（2，﹣4），正方形网格中，每个小正方形的边长是1个单位长度．
①画出△ABC向上平移6个单位得到的△A1B1C1；
②以点C为位似中心，在网格中画出△A2B2C2 ， 使△A2B2C2与△ABC位似，且△A2B2C2与△ABC的位似比为2：1，并直接写出点A2的坐标 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AC=BC，点D、E分别是边AB、AC的中点，将△ADE绕点E旋转180°得△CFE，则四边形ADCF一定是（ ）
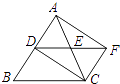
A.矩形
B.菱形
C.正方形
D.梯形 -
科目： 来源： 题型：
查看答案和解析>>【题目】下列式子中正确的是（ ）
A.（
）﹣2=﹣9
B.（﹣2）3=﹣6
C.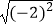
=﹣2
D.（﹣3）0=1 -
科目： 来源： 题型：
查看答案和解析>>【题目】定义：对于一个有理数x，我们把[x]称作x的对称数.
若
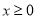，则[x]=x-2:若x<0，则[x]=x+2.例：[1]=1-2=-1，[-2]=-2+2=0（1）求[
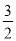][-1]的值；（2）已知有理数a>0.b<0，且满足[a]=[b]，试求代数式
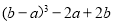的值：（3）解方程：[2x]+[x+1]=1
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，抛物线y=ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．
（1）求抛物线的解析式；
（2）当点P运动到什么位置时，△PAB的面积有最大值？
（3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．
相关试题
