【题目】如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC= . 
参考答案:
【答案】![]()
【解析】解:作EF⊥BC于F,如图,设DE=CE=a,
∵△CDE为等腰直角三角形,
∴CD= ![]() CE=
CE= ![]() a,∠DCE=45°,
a,∠DCE=45°,
∵四边形ABCD为正方形,
∴CB=CD= ![]() a,∠BCD=90°,
a,∠BCD=90°,
∴∠ECF=45°,
∴△CEF为等腰直角三角形,
∴CF=EF= ![]() CE=
CE= ![]() a,在Rt△BEF中,tan∠EBF=
a,在Rt△BEF中,tan∠EBF= ![]() =
=  =
= ![]() ,即∠EBC=
,即∠EBC= ![]() .
.
故答案为 ![]() .
.
作EF⊥BC于F,如图,设DE=CE=a,根据等腰直角三角形的性质得CD= ![]() CE=
CE= ![]() a,∠DCE=45°,再利用正方形的性质得CB=CD=
a,∠DCE=45°,再利用正方形的性质得CB=CD= ![]() a,∠BCD=90°,接着判断△CEF为等腰直角三角形得到CF=EF=
a,∠BCD=90°,接着判断△CEF为等腰直角三角形得到CF=EF= ![]() CE=
CE= ![]() a,然后在Rt△BEF中根据正切的定义求解.本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了等腰直角三角形的性质.
a,然后在Rt△BEF中根据正切的定义求解.本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.也考查了等腰直角三角形的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )

A.50°
B.51°
C.51.5°
D.52.5° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQAC,
其中正确的结论的个数是( )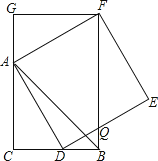
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上.若∠BAD=120°,则弧BC的长度等于 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.
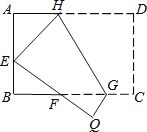
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.

相关试题

