【题目】新知：对角线垂直的四边形两组对边的平方和相等
感知与认证：如图1，2，3中，四边形ABCD中
于O，如图1，AC与BD相互平分，如图2，AC平分BD,结论显然成立.
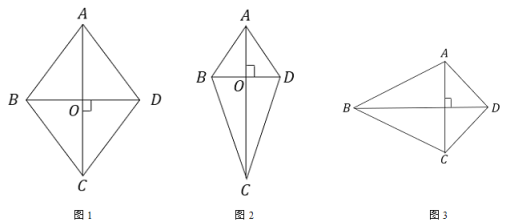
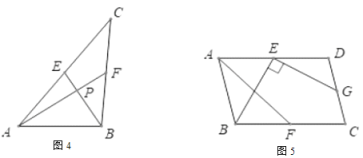
认知证明：（1）请你证明如图3中有
成立。
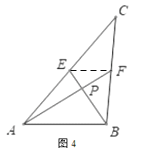
发现应用：（2）如图4，若AF,BE是三角形ABC的中线，
垂足为P
已知：
,
,求AB的长
拓展应用：（3）如图5，在平行四边形ABCD中，点E,F,G分别是AD,BC,CD的中点，
,
，
.求AF的长.
【答案】认识证明：（1）见解析；发现应用：（2）AB=4；拓展应用：（3）
.
【解析】
认识证明：(1)利用勾股定理，分别表示AD2+BC2和AD2+BC2即可证明；发现应用：（2）连接EF,根据中位线的定理可得
,根据中线的定理可得
，结合对角线垂直的四边形两组对边的平方和相等，列出等式，代入值求解即可；拓展应用：（3）连接AC，EF交于H，AC与BE交于点Q，设BE与AF的交点为P.连接PH.可证明EP，AH分别是△AFE的中线，BE⊥AC，结合（2）可求得AF.
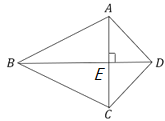
认识证明：（1）如下图：
∵AC⊥BD，
∴∠AED=∠AEB=∠BEC=∠CED=90°，
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2，
AB2+CD2=AE2+BE2+CE2+DE2，
∴AD2+BC2=AB2+CD2.
发现应用：（2）如下图，连接EF
∵AF,BE是三角形ABC的中线
∵
∴
即
解得EF=2，AB=2EF=4.
拓展应用：（3）如图，连接AC，EF交于H，AC与BE交于点Q，设BE与AF的交点为P.连接PH.
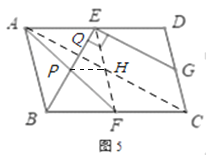
∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC=
，
∴∠EAH=∠FCH.
∵E，F分别是AD，BC的中点，
∵AE∥BF，
∴四边形ABFE是平行四边形，
∴EF=AB=3，AP=PF.
∵在△AEH和△CFH中，
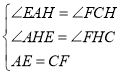
∴△AEH≌△CFH，
∴EH=FH=
，
∴EP，AH分别是△AFE的中线.
∴
∵点E、G分别是AD，CD的中点，
∴EG∥AC.
∵BE⊥EG，
∴BE⊥AC.
∴
即
解得:
,故
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】近两年购物的支付方式日益增多，某数学兴趣小组就此进行了抽样调查，调查结果显示，支付方式有：A微信．B支付宝．C银行卡．D其他．该小组选取了某一超市一天之内购买者的支付方式进行统计，得到如下两幅不完整的统计图．
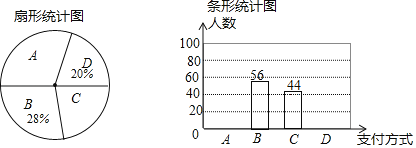
请你根据统计图提供的信息，解答下列问题：
（1）本次调查中，一共调查了多少名购买者？
（2）补全条形统计图：“A微信”支付方式所在扇形的圆心角为 度；
（3）若该超市这一天内有2000名购买者，请你估计B种支付方式的购买者有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数学兴趣小组成员张广益对本年级期中考试数学成绩（成绩取整数，满分为100分）做了统计分析，绘制成如下频数、频率分布表和频数分布直方图．请你根据图表提供的信息，解答下列问题：
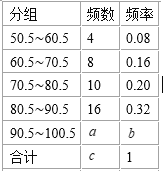
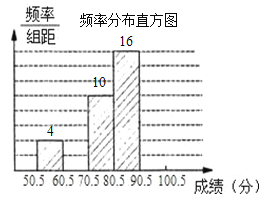
⑴填充频率分布表中的空格：a ，b ，c ；
⑵补全频率分布直方图；
⑶已知本年级共计1700名学生，若竞赛成绩在90分以上(不含90分)为优秀，估算本年级数学成绩优秀的学生约有多少人?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若AC=6，BC=8，OA=2，求线段DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线
，直线
与直线
、
分别相交于C、D两点．
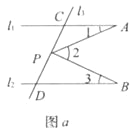
（1）如图a，有一动点P在线段CD之间运动(不与C、D两点重合)，问在点P的运动过程中，是否始终具有∠3+∠1=∠2这一关系，为什么？
（2）如图b，当动点P线段CD之外运动(不与C、D两点重合)，问上述结论是否成立?若不成立，试写出新的结论并说明理由．
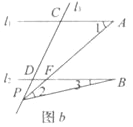
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB=6，BC=4，过对角线BD中点O的直线分别交AB，CD边于点E，F．
（1）求证：四边形BEDF是平行四边形；
（2）当四边形BEDF是菱形时，求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=9，AC=6，BC=12，点M在AB边上，且AM=3，过点M作直线MN与AC边交于点N，使截得的三角形与原三角形相似，则MN=__．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，在四边形ABCD中，AD∥BC，AB∥DC，点E在BC延长线上，连接DE，∠A＋∠E＝180°．
（1）如图1，求证：CD=DE；
（2）如图2，过点C作BE的垂线，交AD于点F，请直接写出BE、AF、DF 之间的数量关系_______________________；
（3）如图3，在（2）的条件下，∠ABC的平分线，交CD于G，交CF于H，连接FG，若∠FGH=45°，DF=8，CH=9，求BE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
