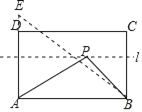
【题目】如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为_____.
S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为_____.

参考答案:
【答案】![]()
【解析】
已知S△PAB=![]() S矩形ABCD ,则可以求出△ABP的高,此题为“将军饮马”模型,过P点作直线l∥AB,作点A关于l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.
S矩形ABCD ,则可以求出△ABP的高,此题为“将军饮马”模型,过P点作直线l∥AB,作点A关于l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.
解:设△ABP中AB边上的高是h.
∵S△PAB=![]() S矩形ABCD,
S矩形ABCD,
∴![]() ABh=
ABh=![]() ABAD,
ABAD,
∴h=![]() AD=2,
AD=2,
∴动点P在与AB平行且与AB的距离是2的直线l上,如图,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.
在Rt△ABE中,∵AB=5,AE=2+2=4,
∴BE=![]() ,
,
即PA+PB的最小值为![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ平行于AB的次数是( )

A.2B.3C.4D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列单项式:
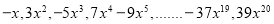 ,回答下列问题:
,回答下列问题:(1)这组单项式的系数符号的规律是 。
(2)这组单项式系数绝对值的规律是 。
(3)这组单项式的次数规律是 。
(4)写出第2017,2018个单项式 , 。
(5)写出第n个单项式 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1) 2(2a 2 9b) 3(3a 2 4b)
(2)(
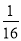 a 2 b2)(
a 2 b2)(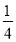 a b)(
a b)( 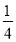 a b)
a b)(3) (
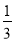 x 2y 3 )2 (3xy)3 (
x 2y 3 )2 (3xy)3 (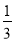 x 2 y 3)2 ( x)3 2 y 3
x 2 y 3)2 ( x)3 2 y 3(4)用简便方法计算:9982 9980 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一节数学课上,老师布置了一个任务:如图1,在Rt△ABC中,∠B=90°,用尺规作图作矩形ABCD.同学们开动脑筋,想出了很多办法,其中小亮作图如图2,他向同学们分享了作法:
①分别以点A、C为圆心,大于
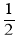 AC长为半径画弧,两弧分别交于点E、F,连接E、F交AC于点O;
AC长为半径画弧,两弧分别交于点E、F,连接E、F交AC于点O;②作射线BO,在BO上取点D,使OD=OB;
③连结AD、CD则四边形ABCD就是所求作的矩形.
请用文字写出小亮的每一步作图的依据① ;② ;③ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列例题的解题过程,再解答下面问题
例题:已知 m n 100 , x y 1 ,求 n x m y 的值
解: n x m y n x m y m n x y 100 1 101
问题:(1)已知 a b 7 , ab 10 ,求 3ab 6a 4b 2a 2ab 的值;
(2)已知 a 2 2ab 2, ab b2 4, 求2a 2
 ab
ab  b2
b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】“智慧南京、绿色出行”,骑共享单车出行已经成为一种时尚.记者随机调查了一些骑共享单车的秦淮区市民,并将他们对各种品牌单车的选择情况绘制成图①和图②的统计图(A:摩拜单车;B:ofo单车;C:HelloBike).请根据图中提供的信息,解答下列问题:

(1)在图①中,C部分所占扇形的圆心角度数为 °;
(2)将图②补充完整;
(3)根据抽样调查结果,请你估计某天该区48万名骑共享单车的市民中有多少名选择摩拜单车?
相关试题

