搜索
【题目】在四边形ABCD中，
，对角线AC平分
．
如图1，若
，
，探究AD、AB与对角线AC三者之间的数量关系，写出结论，不必证明．
如图2若将中的条件“”去掉，中的结论是否还成立？并证明你的结论；
如图3，若
，试探究AD、AB与对角线AC三者之间的数量关系，写出结论，不必证明．
参考答案：
【答案】（1）
；（2）成立；（3）
.
【解析】
结论：
，只要证明
，
即可解决问题；
中的结论成立
以C为顶点，AC为一边作
，
的另一边交AB延长线于点E，只要证明
≌
即可解决问题；
结论：
过点C作
交AB的延长线于点E，只要证明
是等腰直角三角形，≌即可解决问题；
解：
．
理由如下：如图1中，
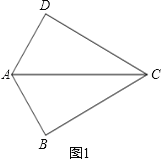
在四边形ABCD中，
，
，
，
，AC平分
，
，
，
，同理
．
．
中的结论成立，理由如下：以C为顶点，AC为一边作
，
的另一边交AB延长线于点E，
，
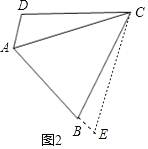
为等边三角形，
，
，
，
，
，
，
，
，
，
≌
，
，
．
结论：
理由如下：
过点C作
交AB的延长线于点E，
，
，
，
，
，
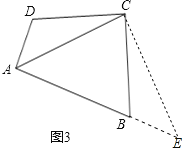
又
平分，
，
．
．
又，
，
≌
，
，
．
在
中，
，
，
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场用36000元购进甲、乙两种商品，销售完后共获利6000元．其中甲种商品每件进价120元，售价138元；乙种商品每件进价100元，售价120元．
（1）该商场购进甲、乙两种商品各多少件？
（2）商场第二次以原进价购进甲、乙两种商品，购进乙种商品的件数不变，而购进甲种商品的件数是第一次的2倍，甲种商品按原售价出售，而乙种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于8160元，乙种商品最低售价为每件多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某住宅小区在施工过程中留下了一块空地，已知AD=8米，CD=6米，∠ADC=90°，AB=26米，BC=24米，小区为美化环境，欲在空地上铺草坪，已知草坪每平方米100元，试问用该草坪铺满这块空地共需花费多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在长度为1个单位长度的小正方形组成的正方形中，点A、B、C在小正方形的顶点上．
（1）在图中画出与△ABC关于直线l成轴对称的△AB′C′；
（2）求△ABC的面积为_______；
（3）在直线l上找一点P，使PB+PC的长最短，则这个最短长度为______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，AB=AC=5，BC=8，若△ABC沿射线BC方向平移m个单位得到△DEF，顶点A，B，C分别与D，E，F对应，若以点A，D，E为顶点的三角形是等腰三角形，则m的值是________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C＝90°，将△ACE沿着AE折叠以后C点正好落在AB边上的点D处．
（1）当∠B＝28°时，求∠AEC的度数；
（2）当AC＝6，AB＝10时，
①求线段BC的长；
②求线段DE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题背景：在△ABC中，AB，BC，AC三边的长分别为
，
，
，求此三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处)，如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
(1)请你将△ABC的面积直接填写在横线上：________.
思维拓展：
(2)我们把上述求△ABC面积的方法叫做构图法．如果△ABC三边的长分别为
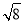a，
a，
a(a＞0)，请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC，并求出它的面积．探索创新：
(3)若△ABC三边的长分别为
，
，
(m＞0，n＞0，且m≠n)，试运用构图法画出示意图并求出这三角形的面积．
相关试题
