【题目】如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D.若AC=9,求AE的值. 
参考答案:
【答案】解:设AE=x,则CE=9﹣x. ∵BE平分∠ABC
又∵CE⊥CB,ED⊥AB
∴DE=CE=9﹣x,
∵DE垂直平分AB,
∴AE=BE,
∴∠A=∠ABE=∠CBE.
∵在RT△ACB中,∠A+∠ABC=90°,
∴∠A=∠ABE=∠CBE=30°,
∴DE= ![]() AE,即9﹣x=
AE,即9﹣x= ![]() x,
x,
∴x=6.
答:AE长为6
【解析】设AE=x,则CE=9﹣x,再根据角平分线的性质得出DE=CE,再根据ED垂直平分AB于D得出AE=BE,在Rt△ACB中由∠A+∠ABC=90°,可知∠A=∠ABE=∠CBE=30°,根据直角三角形的性质即可得出结论.
【考点精析】解答此题的关键在于理解线段垂直平分线的性质的相关知识,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等,以及对含30度角的直角三角形的理解,了解在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A在⊙O上.(不限画图工具,要保留作图痕迹)

(1)作⊙O的内接正三角形ABC.
若⊙O的半径为6,则S扇形OAB=____ ____ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AD=4,CD=3,∠ADC=90°,AB=13,∠ACB=90°,求图形中阴影部分的面积.
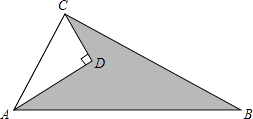
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各数:1,2,5,14 …,按你发现的规律计算这列数的第5个数为_______________
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①2a+b>0;
②b>a>c;③若-1<m<n<1,则m+n<
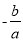 ;④3|a|+|c|<2|b|.其中正确的结论个数是( )
;④3|a|+|c|<2|b|.其中正确的结论个数是( )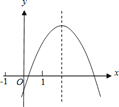
A. ①③④ B. ①③ C. ①④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=∠2,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.试说明:∠BAP+∠BCP=180°.
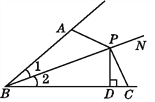
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于
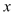 的二次函数y=x2+2kx+k-1,下列说法正确的是( )
的二次函数y=x2+2kx+k-1,下列说法正确的是( )A. 对任意实数k,函数与x轴都没有交点
B. 存在实数n,满足当
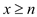 时,函数y的值都随x的增大而减小
时,函数y的值都随x的增大而减小C. 不存在实数n,满足当
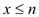 时,函数y的值都随x的增大而减小
时,函数y的值都随x的增大而减小D. 对任意实数k,抛物线
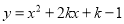 都必定经过唯一定点
都必定经过唯一定点
相关试题

