【题目】如图,∠1=∠2,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.试说明:∠BAP+∠BCP=180°.
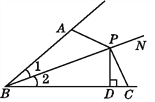
参考答案:
【答案】见解析
【解析】作PE垂直于AB于E,根据角平分线的性质可知PD=PE,HL定理可知△PBD≌△PBE,可得BD=BE,根据题中线段和差的关系,可得△PAE≌△PCD,所以可知∠PAE=∠PCD,根据∠PAE+∠PAB=180°,即可证明题中关系.
证明:如图,过点P作PE⊥BA于E.
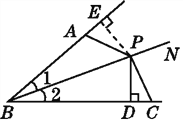
∵PD⊥BC,PE⊥BM,∠1=∠2,
∴PD=PE.
∵PD⊥BC,PE⊥BM,PD=PE,BP=BP,
∴△BPD≌△BPE.
∴BE=BD.
∵AB+BC=2BD,BC=BD+DC,AB=BE-AE,
∴AE=CD.
∵PD=PE,AE=CD,PD⊥BC,PE⊥BM,
∴△PCD≌△PAE,
∴∠PCB=∠PAE.
∵∠BAP+∠PAE=180°,
∴∠BAP+∠PCB=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各数:1,2,5,14 …,按你发现的规律计算这列数的第5个数为_______________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D.若AC=9,求AE的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①2a+b>0;
②b>a>c;③若-1<m<n<1,则m+n<
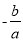 ;④3|a|+|c|<2|b|.其中正确的结论个数是( )
;④3|a|+|c|<2|b|.其中正确的结论个数是( )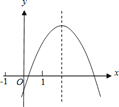
A. ①③④ B. ①③ C. ①④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于
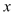 的二次函数y=x2+2kx+k-1,下列说法正确的是( )
的二次函数y=x2+2kx+k-1,下列说法正确的是( )A. 对任意实数k,函数与x轴都没有交点
B. 存在实数n,满足当
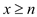 时,函数y的值都随x的增大而减小
时,函数y的值都随x的增大而减小C. 不存在实数n,满足当
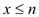 时,函数y的值都随x的增大而减小
时,函数y的值都随x的增大而减小D. 对任意实数k,抛物线
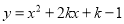 都必定经过唯一定点
都必定经过唯一定点 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线
 截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是三个同学对问题“已知二次函数
 的图象与
的图象与 轴的一个交点坐标是
轴的一个交点坐标是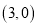 ,你是否也知道二次函数
,你是否也知道二次函数 的图象与
的图象与 轴的一个交点坐标? ”的讨论:
轴的一个交点坐标? ”的讨论:甲说:“这个题目就是求方程
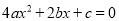 的一个解”;
的一个解”;乙说:“它们的系数有一定的规律,可以试试”;
丙说:“能不能通过换元替换的方法来解决”。参考他们的讨论,你认为二次函数
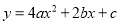 的图象与
的图象与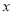 轴的一个交点坐标是 ________________.
轴的一个交点坐标是 ________________.
相关试题

