【题目】(1)引入:
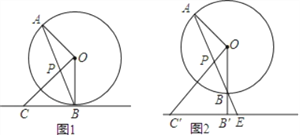
如图1,直线AB为⊙O的弦,OC⊥OA,交AB于点P,且PC=BC,直线BC是否与⊙O相切,为什么?
(2)引申:
如图2,记(1)中⊙O的切线为直线l,在(1)的条件下,将切线l向下平移,设平移后的直线l与OB的延长线相交于点B′,与AB的延长线相交于点E,与OP的延长线相交于点C′,找出图2中与C′P相等的线段,并说明理由.
参考答案:
【答案】(1)相切,(2)C′P=C′E.
【解析】试题分析:(1)由OC⊥OA,易得∠APO+∠OAB=90°,然后由等腰三角形的性质可得∠OAB=∠ABO,∠CBP=∠CPB,等量代换可得∠CBP+∠OBA=90°,即∠OBC-90°,由切线的判定可得出结论;
(2)由(1)可得∠OAB+∠C′PE=90°,等量代换可得∠ABO+∠C′PE=90°,由∠EBB′+∠BEB′=90°,∠EBB′=∠ABO,易得∠C′PE=∠BEB′,得出结论.
试题解析:(1)相切,
∵OC⊥OA,
∴∠AOC=90°,
∴∠APO+∠OAB=90°,
∵OA=OB,
∴∠OAB=∠ABO,
∵PC=PB,
∴∠CBP=∠CPB,
∵∠APO=∠CPB,
∴∠CBP+∠OBA=90°,
即∠OBC=90°,
∴OB⊥BC
∵OB为半径,
∴BC与⊙O相切;
(2)C′P=C′E,
∵∠OB′C′=90°,∠APO+∠OAB=90°,且∠APO=∠C′PE,
∴∠OAB+∠C′PE=90°,
∵OA=OB,
∴∠OAB=∠ABO,
∴∠ABO+∠C′PE=90°,
∵∠EBB′+∠BEB′=90°,且∠EBB′=∠ABO,
∴∠C′PE=∠BEB′,
∴C′P=C′E.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平整地面上,若干个完全相同的棱长为10cm的小正方体堆成一个几何体.
(1)这个几何体由______个小正方体组成.
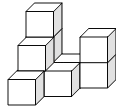
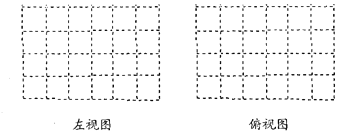
(2)在下面网格中画出左视图和俯视图.
(3)如果在这个几何体的表面(不含底面)喷上黄色的漆,则这个几何体喷漆的面积是多少cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.
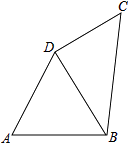
(1)求∠BDC的度数;
(2)四边形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两边分别是4和9,则这个等腰三角形的周长是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个凸多边形每一个内角都是135°,则这个多边形是____边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一个长方体切去一个角后,剩下的几何体的顶点个数为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
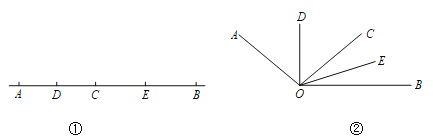
相关试题

