【题目】通过小学的学习我们知道,分数可分为“真分数”和“假分数”,并且假分数都可化为带分数.类比分数,对于分式也可以定义:对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).
如:![]()
解决下列问题:
(1)分式![]() 是________分式(填“真”或“假”);
是________分式(填“真”或“假”);
(2)假分式![]() 可化为带分式_________的形式;请写出你的推导过程;
可化为带分式_________的形式;请写出你的推导过程;
(3)如果分式![]() 的值为整数,那么
的值为整数,那么![]() 的整数值为_________.
的整数值为_________.
参考答案:
【答案】![]() 真
真
![]()
![]()
【解析】
(1)比较分式![]() 的分子分母的次数容易判定出它是真分式还是假分式;
的分子分母的次数容易判定出它是真分式还是假分式;
(2)分式分子![]() 变形为
变形为![]() ,利用同分母分式减法逆运算法则变形即可得;
,利用同分母分式减法逆运算法则变形即可得;
(3)在![]() 的基础上,对于这个带分式,只要满足
的基础上,对于这个带分式,只要满足![]() 为整数即可求出整数x的值.
为整数即可求出整数x的值.
(1)分式![]() 的分子是常数,其次数为0,分母x的次数为1,分母的次数大于分子的次数,所以是真分;
的分子是常数,其次数为0,分母x的次数为1,分母的次数大于分子的次数,所以是真分;
(2) ![]() ;
;
(3)由(2)得:![]() ,当
,当![]() 为整数时,原分式的值为整数,
为整数时,原分式的值为整数,
∴此时,整数x可能满足:![]() 或
或![]() 或
或![]() 或
或![]()
∴![]() .
.
故答案为:![]() 真;
真;![]() ;
;![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一张三角形纸片ABC,∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两张纸片均为等腰三角形,则∠C的度数可以是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3
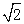 ,求弦AD的长.
,求弦AD的长.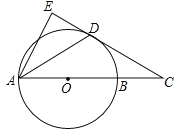
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
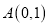 .规定“把点
.规定“把点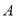 先作关于
先作关于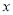 轴对称,再向左平移1个单位”为一次变化.经过第一次变换后,点
轴对称,再向左平移1个单位”为一次变化.经过第一次变换后,点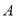 的坐标为_______;经过第二次变换后,点
的坐标为_______;经过第二次变换后,点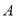 的坐标为_____;那么连续经过2019次变换后,点
的坐标为_____;那么连续经过2019次变换后,点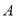 的坐标为_______.
的坐标为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(m,n)(m<0,
n>0),E点在边BC上,F点在边OA上.将矩形OABC沿EF折叠,点B正好与点O重合,双曲线
 过点E.
过点E.(1) 若m=-8,n =4,直接写出E、F的坐标;
(2) 若直线EF的解析式为
 ,求k的值;
,求k的值;(3) 若双曲线
 过EF的中点,直接写出tan∠EFO的值.
过EF的中点,直接写出tan∠EFO的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角梯形ABCD中,AB⊥BC,AD∥BC,点P为DC上一点,且AP=AB,过点C作CE⊥BP交直线BP于E.
(1) 若
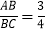 ,求证:
,求证: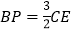 ;
;(2) 若AB=BC.
① 如图2,当点P与E重合时,求
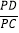 的值;
的值;② 如图3,设∠DAP的平分线AF交直线BP于F,当CE=1,
 时,直接写出线段AF的长.
时,直接写出线段AF的长.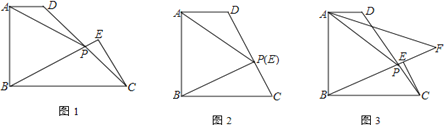
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合实践
如图①,
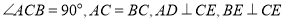 ,垂足分别为点
,垂足分别为点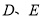 ,
,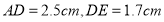 .
.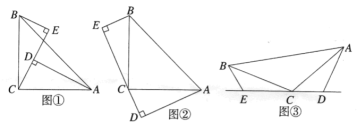
(1)求
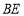 的长;
的长;(2)将
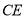 所在直线旋转到
所在直线旋转到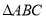 的外部,如图②,猜想
的外部,如图②,猜想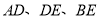 之间的数量关系,直接写出结论,不需证明;
之间的数量关系,直接写出结论,不需证明;(3)如图③,将图①中的条件改为:在
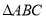 中,
中,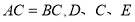 三点在同一直线上,并且
三点在同一直线上,并且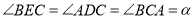 ,其中
,其中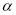 为任意钝角.猜想
为任意钝角.猜想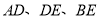 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
相关试题

