【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(m,n)(m<0,
n>0),E点在边BC上,F点在边OA上.将矩形OABC沿EF折叠,点B正好与点O重合,双曲线![]() 过点E.
过点E.
(1) 若m=-8,n =4,直接写出E、F的坐标;
(2) 若直线EF的解析式为![]() ,求k的值;
,求k的值;
(3) 若双曲线![]() 过EF的中点,直接写出tan∠EFO的值.
过EF的中点,直接写出tan∠EFO的值.

参考答案:
【答案】(1)E(-3,4)、F(-5,0);(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1) 连接OE,BF,根据题意可知:![]() 设
设![]() 则
则![]() 根据勾股定理可得:
根据勾股定理可得:![]() 即
即![]() 解得:
解得:![]() 即可求出点E的坐标,同理求出点F的坐标.
即可求出点E的坐标,同理求出点F的坐标.
(2) 连接BF、OE,连接BO交EF于G由翻折可知:GO=GB,BE=OE,证明△BGE≌△OGF,证明四边形OEBF为菱形,令y=0,则![]() ,解得
,解得![]() , 根据菱形的性质得OF=OE=BE=BF=
, 根据菱形的性质得OF=OE=BE=BF=![]() 令y=n,则
令y=n,则![]() ,解得
,解得![]() 则CE=
则CE=![]() ,在Rt△COE中, 根据勾股定理列出方程
,在Rt△COE中, 根据勾股定理列出方程![]() ,即可求出点E的坐标,即可求出k的值;
,即可求出点E的坐标,即可求出k的值;
(3) 设EB=EO=x,则CE=-m-x,在Rt△COE中,根据勾股定理得到(-m-x)2+n2=x2,解得![]() ,求出点E(
,求出点E(![]() )、F(
)、F(![]() ),根据中点公式得到EF的中点为(
),根据中点公式得到EF的中点为(![]() ),将E(
),将E(![]() )、(
)、(![]() )代入
)代入![]() 中,得
中,得![]() ,得m2=2n2
,得m2=2n2
即可求出tan∠EFO=![]() .
.
解:(1)如图:连接OE,BF,

E(-3,4)、F(-5,0)
(2) 连接BF、OE,连接BO交EF于G由翻折可知:GO=GB,BE=OE

可证:△BGE≌△OGF(ASA)
∴BE=OF
∴四边形OEBF为菱形
令y=0,则![]() ,解得
,解得![]() ,∴OF=OE=BE=BF=
,∴OF=OE=BE=BF=![]()
令y=n,则![]() ,解得
,解得![]() ∴CE=
∴CE=![]()
在Rt△COE中,![]() ,
,
解得![]()
∴E(![]() )
)
∴![]()
(3) 设EB=EO=x,则CE=-m-x,
在Rt△COE中,(-m-x)2+n2=x2,解得![]()
∴E(![]() )、F(
)、F(![]() )
)
∴EF的中点为(![]() )
)
将E(![]() )、(
)、(![]() )代入
)代入![]() 中,得
中,得
![]() ,得m2=2n2
,得m2=2n2
∴tan∠EFO=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3
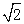 ,求弦AD的长.
,求弦AD的长.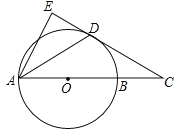
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
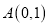 .规定“把点
.规定“把点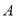 先作关于
先作关于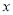 轴对称,再向左平移1个单位”为一次变化.经过第一次变换后,点
轴对称,再向左平移1个单位”为一次变化.经过第一次变换后,点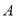 的坐标为_______;经过第二次变换后,点
的坐标为_______;经过第二次变换后,点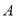 的坐标为_____;那么连续经过2019次变换后,点
的坐标为_____;那么连续经过2019次变换后,点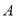 的坐标为_______.
的坐标为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过小学的学习我们知道,分数可分为“真分数”和“假分数”,并且假分数都可化为带分数.类比分数,对于分式也可以定义:对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).
如:
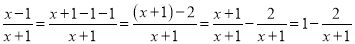
解决下列问题:
(1)分式
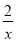 是________分式(填“真”或“假”);
是________分式(填“真”或“假”);(2)假分式
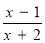 可化为带分式_________的形式;请写出你的推导过程;
可化为带分式_________的形式;请写出你的推导过程;(3)如果分式
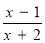 的值为整数,那么
的值为整数,那么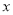 的整数值为_________.
的整数值为_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角梯形ABCD中,AB⊥BC,AD∥BC,点P为DC上一点,且AP=AB,过点C作CE⊥BP交直线BP于E.
(1) 若
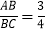 ,求证:
,求证: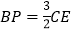 ;
;(2) 若AB=BC.
① 如图2,当点P与E重合时,求
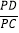 的值;
的值;② 如图3,设∠DAP的平分线AF交直线BP于F,当CE=1,
 时,直接写出线段AF的长.
时,直接写出线段AF的长.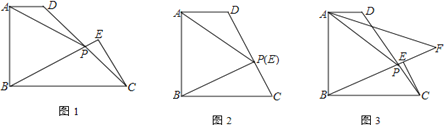
-
科目: 来源: 题型:
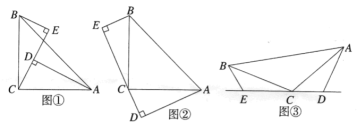
查看答案和解析>>【题目】综合实践
如图①,
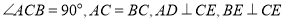 ,垂足分别为点
,垂足分别为点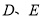 ,
,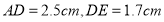 .
.
(1)求
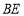 的长;
的长;(2)将
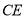 所在直线旋转到
所在直线旋转到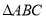 的外部,如图②,猜想
的外部,如图②,猜想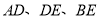 之间的数量关系,直接写出结论,不需证明;
之间的数量关系,直接写出结论,不需证明;(3)如图③,将图①中的条件改为:在
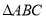 中,
中,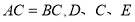 三点在同一直线上,并且
三点在同一直线上,并且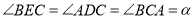 ,其中
,其中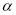 为任意钝角.猜想
为任意钝角.猜想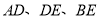 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】(11·孝感)学生甲与学生乙玩一种转盘游戏.如图是两个完全相同的转盘,每个转盘被分成面积相等的四个区域,分别用数字“1”、“2”、“3”、“4”表示.固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若指针指向扇形的分界线,则都重转一次.在该游戏中乙获胜的概率是 ( )
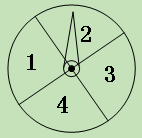
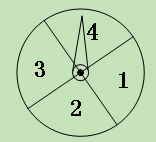
A.
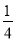 B.
B.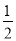 C.
C.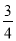 D.
D.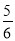
相关试题

