【题目】在平面直角坐标系中,点![]() 为坐标原点,已知点
为坐标原点,已知点![]() ,将
,将![]() 绕坐标原点
绕坐标原点![]() 旋转90°到
旋转90°到![]() ,则点
,则点![]() 的坐标是__________.
的坐标是__________.
参考答案:
【答案】![]() 或
或![]()
【解析】
根据题意作图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,根据旋转的性质可得OA=OA′,利用同角的余角相等求出∠OAB=∠A′OB′,然后利用“角角边”证明△AOB和△OA′B′全等,根据全等三角形对应边相等可得OB′=AB,A′B′=OB,然后写出点A′的坐标,同理求出逆时针旋转90![]() 时A′的坐标,故可求解.
时A′的坐标,故可求解.
如图,过点A作AB⊥x轴于B,过点A′作A′B′⊥x轴于B′,

∵OA绕坐标原点O顺时针旋转90![]() 至OA′,
至OA′,
∴OA=OA′,∠AOA′=90![]() ,
,
∵∠A′OB′+∠AOB=90![]() ,∠AOB+∠OAB=90
,∠AOB+∠OAB=90![]() ,
,
∴∠OAB=∠A′OB′,
在△AOB和△OA′B′中,
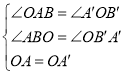 ,
,
∴△AOB≌△OA′B′(AAS),
∴OB′=AB=4,A′B′=OB=3,
∴点A′的坐标为(4,3).
同理OA绕坐标原点O逆时针旋转90![]() 至OA′
至OA′
OB’=AB=4,A’B’=OB=3
∴点A′的坐标为(-4,3).
综上,点A′的坐标为(4,3)或(-4,3).
故答案为:![]() 或
或![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标的数值分别为-7、-1、3,乙袋中的三张卡片上所标的数值分别为-2、1、6.先从甲袋中随机取出一张卡片,用
 表示取出的卡片上标的数值,再从乙袋中随机取出一张卡片,用
表示取出的卡片上标的数值,再从乙袋中随机取出一张卡片,用  表示取出的卡片上标的数值,把
表示取出的卡片上标的数值,把  、
、  分别作为点
分别作为点  的横坐标、纵坐标.
的横坐标、纵坐标.
(1)用适当的方法写出点 的所有情况;
的所有情况;
(2)求点 落在第三象限的概率.
落在第三象限的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13 个结,然后以3个结间距、4 个结间距、5 个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
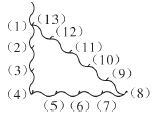
A.直角三角形两个锐角互补
B.三角形内角和等于180°
C.三角形两条短边的平方和等于长边的平方
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明过程.
如图,已知,∠1+∠2=180°,∠A=∠D.求证AB∥CD.
证明:∵∠1+∠2=180°(已知)
∠1=∠3( )
∴∠3+∠2=180°( )
∴AE∥ ( )
∴∠D= ( )
∵∠A=∠D(已知)
∴∠A=∠CEA( )
∴AB∥CD ( )

-
科目: 来源: 题型:
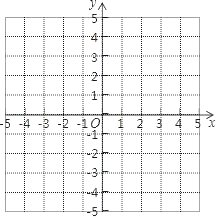
查看答案和解析>>【题目】在下面所给的平面直角坐标系中,解答下列问题
(1)描出点A(﹣2,0),B(2,﹣1),C(3,3),并用线段依次连接起来.
(2)将三角形ABC向左平移2个单位长度,再向下平移3个单位长度,得到三角形A′B′C′.
(3)写出三角形A′B′C′各个顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.

(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,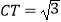 ,求AD的长.
,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,反比例函数
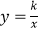 的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).
的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).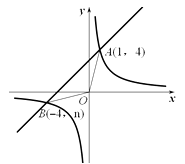
(1)求△OAB的面积;
(2)根据图象,直接写出不等式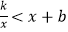 的解集.
的解集.
相关试题

