【题目】甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标的数值分别为-7、-1、3,乙袋中的三张卡片上所标的数值分别为-2、1、6.先从甲袋中随机取出一张卡片,用 ![]() 表示取出的卡片上标的数值,再从乙袋中随机取出一张卡片,用
表示取出的卡片上标的数值,再从乙袋中随机取出一张卡片,用 ![]() 表示取出的卡片上标的数值,把
表示取出的卡片上标的数值,把 ![]() 、
、 ![]() 分别作为点
分别作为点 ![]() 的横坐标、纵坐标.
的横坐标、纵坐标.
(1)用适当的方法写出点 ![]() 的所有情况;
的所有情况;
(2)求点 ![]() 落在第三象限的概率.
落在第三象限的概率.
参考答案:
【答案】
(1)解:如下表,
﹣7 | ﹣1 | 3 | |
﹣2 | (﹣7,﹣2) | (﹣1,﹣2) | ( 3,﹣2) |
1 | (﹣7,1) | (﹣1,1) | ( 3,1) |
6 | (﹣7,6) | (﹣1,6) | (3,6) |
点A(x,y)共9种情况为:(-7,-2);(-7,1);(-7,6);(-1,-2);(-1,1);(-1,6);(3,-2);(3,1);(3,6)
(2)解: ∵点A落在第三象限共有(﹣7,﹣2)(﹣1,﹣2)两种情况,
∴点A落在第三象限的概率是 ![]()
【解析】(1)事件分为两个步骤,每个步骤有3种情况,共9种情况;(2)关注的结果有2种,代入概率公式中即可求出概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来随着全国楼市的降温,商品房的价格开始呈现下降趋势,2012年某楼盘平均售价为5000元/平方米,2014年该楼盘平均售价为4050元/平方米.
(1)如果该楼盘2013年和2014年楼价平均下降率相同,求该楼价的平均下降率;
(2)按照(1)中楼价的下降速度,请你预测该楼盘2015年楼价平均是多少元/平方米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)求证:AM=AD+MC;
(2)若AD=4,求AM的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)在Rt△ABC中,∠BAC=
 ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
-
科目: 来源: 题型:
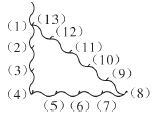
查看答案和解析>>【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13 个结,然后以3个结间距、4 个结间距、5 个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
A.直角三角形两个锐角互补
B.三角形内角和等于180°
C.三角形两条短边的平方和等于长边的平方
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明过程.
如图,已知,∠1+∠2=180°,∠A=∠D.求证AB∥CD.
证明:∵∠1+∠2=180°(已知)
∠1=∠3( )
∴∠3+∠2=180°( )
∴AE∥ ( )
∴∠D= ( )
∵∠A=∠D(已知)
∴∠A=∠CEA( )
∴AB∥CD ( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
 为坐标原点,已知点
为坐标原点,已知点 ,将
,将 绕坐标原点
绕坐标原点 旋转90°到
旋转90°到 ,则点
,则点 的坐标是__________.
的坐标是__________.
相关试题

