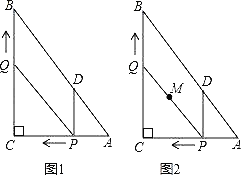
【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
参考答案:
【答案】(1)8-2t, ![]() .(2)不存在;当点Q的速度为每秒
.(2)不存在;当点Q的速度为每秒![]() 个单位长度时,经过
个单位长度时,经过![]() 秒,四边形PDBQ是菱形.(3)线段PQ中点M所经过的路径长为2
秒,四边形PDBQ是菱形.(3)线段PQ中点M所经过的路径长为2![]() 单位长度.
单位长度.
【解析】试题分析:(1)根据题意得:CQ=2t,PA=t,由Rt△ABC中,∠C=90°,AC=6,BC=8,PD∥BC,即可得tanA=![]() ,则可求得QB与PD的值;
,则可求得QB与PD的值;
(2)易得△APD∽△ACB,即可求得AD与BD的长,由BQ∥DP,可得当BQ=DP时,四边形PDBQ是平行四边形,即可求得此时DP与BD的长,由DP≠BD,可判定PDBQ不能为菱形;然后设点Q的速度为每秒v个单位长度,由要使四边形PDBQ为菱形,则PD=BD=BQ,列方程即可求得答案;
(3)设E是AC的中点,连接ME.当t=4时,点Q与点B重合,运动停止.设此时PQ的中点为F,连接EF,由△PMN∽△PQC.利用相似三角形的对应边成比例,即可求得答案.
试题解析:(1)根据题意得:CQ=2t,PA=t,
∴QB=8-2t,
∵在Rt△ABC中,∠C=90°,AC=6,BC=8,PD∥BC,
∴∠APD=90°,
∴tanA=![]() ,
,
∴PD= ![]() .
.
(2)不存在
在Rt△ABC中,∠C=90°,AC=6,BC=8,
∴AB=10
∵PD∥BC,
∴△APD∽△ACB,
∴![]() ,即
,即![]() ,
,
∴AD= ![]() ,
,
∴BD=AB-AD=10- ![]() ,
,
∵BQ∥DP,
∴当BQ=DP时,四边形PDBQ是平行四边形,
即8-2t= ![]() ,解得:t=
,解得:t=![]() .
.
当t=![]() 时,PD=
时,PD=![]() ,BD=10-
,BD=10-![]() ,
,
∴DP≠BD,
∴PDBQ不能为菱形.
设点Q的速度为每秒v个单位长度,
则BQ=8-vt,PD= ![]() ,BD=10-
,BD=10- ![]() ,
,
要使四边形PDBQ为菱形,则PD=BD=BQ,
当PD=BD时,即![]() =10-
=10- ![]() ,解得:t=
,解得:t=![]()
当PD=BQ,t=![]() 时,即
时,即![]() ,解得:v=
,解得:v=![]()
当点Q的速度为每秒![]() 个单位长度时,经过
个单位长度时,经过![]() 秒,四边形PDBQ是菱形.
秒,四边形PDBQ是菱形.

(3)如图2,以C为原点,以AC所在的直线为x轴,建立平面直角坐标系.
依题意,可知0≤t≤4,当t=0时,点M1的坐标为(3,0),当t=4时点M2的坐标为(1,4).
设直线M1M2的解析式为y=kx+b,
∴![]() ,
,
解得
![]() ,
,
∴直线M1M2的解析式为y=-2x+6.
∵点Q(0,2t),P(6-t,0)
∴在运动过程中,线段PQ中点M3的坐标(![]() ,t).
,t).
把x=![]() 代入y=-2x+6得y=-2×
代入y=-2x+6得y=-2×![]() +6=t,
+6=t,
∴点M3在直线M1M2上.
过点M2作M2N⊥x轴于点N,则M2N=4,M1N=2.
∴M1M2=2![]()
∴线段PQ中点M所经过的路径长为2![]() 单位长度.
单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我省某地区为了了解2016年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.读普通高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图(如图1,如图2)
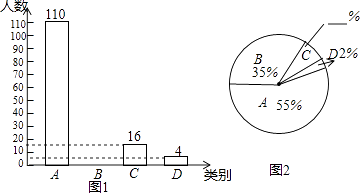
(1)填空:该地区共调查了 200 名九年级学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该地区2016年初中毕业生共有3500人,请估计该地区今年初中毕业生中读普通高中的学生人数;
(4)老师想从甲,乙,丙,丁4位同学中随机选择两位同学了解他们毕业后的去向情况,请用画树状图或列表的方法求选中甲同学的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,直线l1经过(2,3)和(﹣1,﹣3),直线l2经过原点O,且与直线l1交于点P(﹣2,a).
(1)求a的值;
(2)(﹣2,a)可看成怎样的二元一次方程组的解?
(3)设直线l1与y轴交于点A,你能求出△APO的面积吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.

(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC=(填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为(用含n的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,
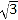 ),点C的坐标为(
),点C的坐标为( ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
A.
 B.
B.  C.
C.  D. 2
D. 2 
-
科目: 来源: 题型:
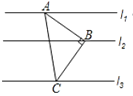
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3.若l1与l2的距离为4,l2与l3的距离为6,则Rt△ABC的面积为___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
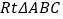 中,
中,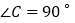 ,把
,把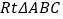 绕着
绕着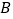 点逆时针旋转,得到
点逆时针旋转,得到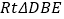 ,点
,点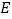 在
在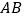 上.
上.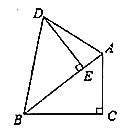
(1)若
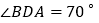 ,求得
,求得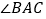 度数;
度数;(2)若
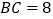 ,
,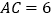 ,求
,求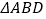 中
中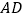 边上的高.
边上的高.
相关试题

