【题目】联想我们曾经学习过的三角形外心的概念,我们可引入准外心的定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.请回答下面的三个问题:

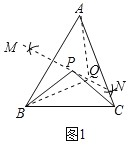
(1)如图1,若PB=PC,则点P为△ABC的准外心,而且我们知道满足此条件的准外心有无数多个,你能否用尺规作出另外一个准外心Q呢?请尝试完成;
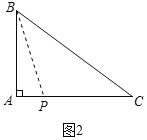
(2)如图2,已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长;
(3)如图3,点B既是△EDC又是△ADC的准外心,BD=BA=BC=2AD,BD∥AC,CD=![]() ,求AD的值.
,求AD的值.
参考答案:
【答案】(1)能用尺规作出另外一个准外心Q,如图1所示:点Q为△ABC的准外心;(2)准外心P在AC边上,PA的长为![]() 或2;(3)AD=
或2;(3)AD=![]() .
.
【解析】
(1)作AB的垂直平分线MN,在MN上取点Q即可;
(2)连接BP,由勾股定理得出AC=4,分三种情况讨论,由直角三角形的性质即可得出答案;
(3)由BD=BA=BC,得出∠BAC=∠BCA,点D、A、C在以B为圆心,AB长为半径的圆上,由圆周角定理得出∠ABD=2∠ACD,作BE⊥CD于E,BF⊥AD于F,由垂径定理得出DE=CE![]() CD
CD![]() ,DF=AF
,DF=AF![]() AD,∠ABD=2∠DBF,∠BEC=∠DFB=90°,证明△BDF≌△CBE,得出DF=BE,设DF=x,则BE=x,AD=2x,BD=2AD=4x.在Rt△BDE中,由勾股定理得出方程,解方程即可.
AD,∠ABD=2∠DBF,∠BEC=∠DFB=90°,证明△BDF≌△CBE,得出DF=BE,设DF=x,则BE=x,AD=2x,BD=2AD=4x.在Rt△BDE中,由勾股定理得出方程,解方程即可.
(1)能用尺规作出另外一个准外心Q,
作AB的垂直平分线MN,在MN上取点Q,如图1所示:
则QA=QB,点Q为△ABC的准外心;
(2)连接BP,如图2所示:
∵△ABC为直角三角形,斜边BC=5,AB=3,
∴AC![]() 4.
4.
∵准外心P在AC边上,
①当PB=PC时,
设PB=x,则PC=x,PA=4﹣x,
在Rt△ABP中,由勾股定理得:32+(4﹣x)2=x2,
解得:x![]() ,
,
∴PA=4![]() ;
;
②当PA=PC时,PA![]() AC=2;
AC=2;
③当PA=PB时.
∵△ABC是直角三角形,∴此情况不存在.
综上所述:准外心P在AC边上,PA的长为![]() 或2;
或2;
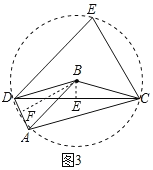
(3)∵BD=BA=BC,∴∠BAC=∠BCA,点D、A、C在以B为圆心,AB长为半径的圆上,如图3所示,则∠ABD=2∠ACD.
作BE⊥CD于E,BF⊥AD于F,
则DE=CE![]() CD
CD![]() ,DF=AF
,DF=AF![]() AD,
AD,
∠ABD=2∠DBF,∠BEC=∠DFB=90°.
∵BD∥AC,
∴∠ABD=∠BAC=∠BCA=2∠ACD=2∠DBF=2∠BCE,
∴∠DBF=∠BCE.
在△BDF和△CBE中,∵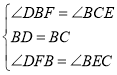 ,
,
∴△BDF≌△CBE(ASA),∴DF=BE.
设DF=x,则BE=x,AD=2x,BD=2AD=4x,
在Rt△BDE中,由勾股定理得:x2+(![]() )2=(4x)2,
)2=(4x)2,
解得:x![]() ,∴AD=2x
,∴AD=2x![]() .
.
-
科目: 来源: 题型:
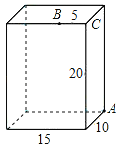
查看答案和解析>>【题目】如图,一个放置在地面上的长方体,长为15cm,宽为10cm,高为20cm,点B与点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,BE与CD交于点G.

(1)求证:AP=DG;
(2)求线段AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点P从点C出发沿线段CA以每秒2cm的速度运动,同时点Q从点B出发沿线段BC以每秒1cm的速度运动.设运动时间为t秒(0<t<5).
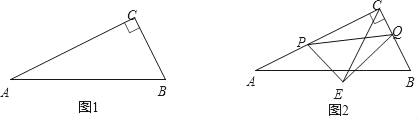
(1)填空:AB= cm;
(2)t为何值时,△PCQ与△ACB相似;
(3)如图2,以PQ为斜边在异于点C的一侧作Rt△PEQ,且
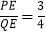 ,连结CE,求CE.(用t的代数式表示).
,连结CE,求CE.(用t的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,分别以A和B为圆心,大于
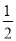 AB的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AB、AC于点F、D,作DE⊥BC于E.有下面三个结论:①BD平分∠ABC;②DE=DF;③BC+CD=2AF;其中,正确的结论的个数是( )
AB的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AB、AC于点F、D,作DE⊥BC于E.有下面三个结论:①BD平分∠ABC;②DE=DF;③BC+CD=2AF;其中,正确的结论的个数是( )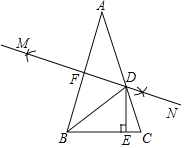
A.3B.2C.1D.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形
 为菱形,点
为菱形,点 ,
, 的坐标分别为
的坐标分别为 、
、 ,动点
,动点 从点
从点 出发,以每秒
出发,以每秒 个单位的速度沿
个单位的速度沿 向终点
向终点 运动,连接
运动,连接 并延长交
并延长交 于点
于点 ,过点
,过点 作
作 ,交
,交 于点
于点 ,连接
,连接 ,当动点
,当动点 运动了
运动了 秒时.
秒时.(1)
 点的坐标为________,
点的坐标为________, 点的坐标为________(用含
点的坐标为________(用含 的代数式表示);
的代数式表示);(2)记
 的面积为
的面积为 ,求
,求 与
与 的函数关系式
的函数关系式 ,并求出当
,并求出当 取何值时,
取何值时, 有最大值,最大值是多少?
有最大值,最大值是多少?(2)在
 出发的同时,有一动点
出发的同时,有一动点 从
从 点开始在线段
点开始在线段 上以每秒
上以每秒 个单位长度的速度向点
个单位长度的速度向点 移动,试求当
移动,试求当 为何值时,
为何值时, 与
与 相似.
相似.
相关试题

