【题目】如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.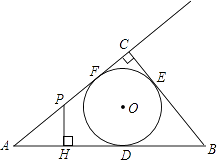
(1)直接写出线段AC、AD及⊙O半径的长;
(2)设PH=x,PC=y,求y关于x的函数关系式;
(3)当PH与⊙O相切时,求相应的y值.
参考答案:
【答案】
(1)
解:AC=4,AD=3,⊙O的半径长为1.
(如图1,连接AO、DO.

设⊙O的半径为r.
在Rt△ABC中,由勾股定理得AC= ![]() =4,
=4,
则⊙O的半径r= ![]() (AC+BC﹣AB)=
(AC+BC﹣AB)= ![]() ×(4+3﹣5)=1;
×(4+3﹣5)=1;
∵CE、CF是⊙O的切线,∠ACB=90°,
∴∠CFO=∠FCE=∠CEO=90°,OF=OE,
∴四边形CEOF是正方形,
∴CF=OF=1;
又∵AD、AF是⊙O的切线,
∴AF=AD;
∴AF=AC﹣CF=AC﹣OF=4﹣1=3,即AD=3);
(2)
解:①如图1,若点P在线段AC上时.
在Rt△ABC中,AB=5,AC=4,BC=3,
∵∠C=90°,PH⊥AB,
∴∠C=∠PHA=90°,
∵∠A=∠A,
∴△AHP∽△ACB,
∴ ![]() ,
,
即 ![]() ,
,
∴y=﹣ ![]() x+4,即y与x的函数关系式是y=﹣
x+4,即y与x的函数关系式是y=﹣ ![]() x+4(0≤x≤2.4);
x+4(0≤x≤2.4);
②同理,当点P在线段AC的延长线上时,△AHP∽△ACB,
则 ![]() ,
,
即 ![]() ,
,
∴y= ![]() x﹣4,即y与x的函数关系式是y=
x﹣4,即y与x的函数关系式是y= ![]() x﹣4(x>2.4);
x﹣4(x>2.4);
(3)
解:①当点P在线段AC上时,如图2,P′H′与⊙O相切于点M.
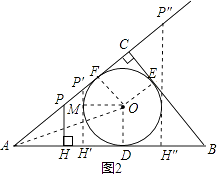
∵∠OMH′=∠MH′D=∠H′DO=90°,OM=OD,
∴四边形OMH′D是正方形,
∴MH′=OM=1;
由(1)知,四边形CFOE是正方形,
CF=OF=1,
∴P′H′=P′M+MH′=P′F+FC=P′C,即x=y;
又由(2)知,y=﹣ ![]() x+4,
x+4,
∴y=﹣ ![]() y+4,
y+4,
解得y= ![]() .
.
②当点P在AC的延长线上时,如图,P″H″与⊙O相切.此时y=1.
【解析】(1)由勾股定理求AC的长度;设⊙O的半径为r,则r= ![]() (AC+BC﹣AB);根据圆的切线定理、正方形的判定定理知四边形CEOF是正方形;然后由正方形的性质证得CF=OF=1,则由图中线段间的和差关系即可求得AD的长度;(2)分类讨论:①当点P在线段AC上时,通过相似三角形△AHP∽△ACB的对应边成比例知,
(AC+BC﹣AB);根据圆的切线定理、正方形的判定定理知四边形CEOF是正方形;然后由正方形的性质证得CF=OF=1,则由图中线段间的和差关系即可求得AD的长度;(2)分类讨论:①当点P在线段AC上时,通过相似三角形△AHP∽△ACB的对应边成比例知, ![]() ,将“PH=x,PC=y”代入求出即可求得y关于x的函数关系式;②当点P在线段AC的延长线上时,同理,利用相似三角形的性质求得y关于x的函数关系式;(3)根据圆的切线定理证得四边形OMH′D、四边形CFOE为正方形;然后利用正方形的性质、圆的切线定理推知P′H′=P′M+MH′=P′F+FC=P′C,即x=y;最后将其代入(2)中的函数关系式即可求得y值.
,将“PH=x,PC=y”代入求出即可求得y关于x的函数关系式;②当点P在线段AC的延长线上时,同理,利用相似三角形的性质求得y关于x的函数关系式;(3)根据圆的切线定理证得四边形OMH′D、四边形CFOE为正方形;然后利用正方形的性质、圆的切线定理推知P′H′=P′M+MH′=P′F+FC=P′C,即x=y;最后将其代入(2)中的函数关系式即可求得y值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G.
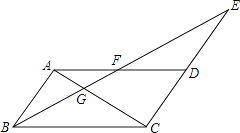
(1)求证:AF=DF;
(2)若BC=2AB,DE=1,∠ABC=60°,求FG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某苹果生产基地,用30名工人进行采摘或加工苹果 ,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售;另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4 000元;加工成罐头出售每吨获利10 000元.采摘的工人每人可采摘苹果0.4吨;加工罐头的工人每人可加工0.3吨.设有x名工人进行苹果采摘,全部售出后,总利润为y元.
(1)求y与x的函数关系式;
(2)如何分配工人才能获利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司决定利用仅有的349个甲种部件和295个乙种部件组装A、B两种型号的简易板房共50套捐赠给灾区.已知组装一套A型号简易板房需要甲种部件8个和乙种部件4个,组装一套B型号简易板房需要甲种部件5个和乙种部件9个.
(1)该公司组装A、B两种型号的简易板房时,共有多少种组装方案?
(2)若组装A、B两种型号的简易板房所需费用分别为每套200元和180元,问最少总组装费用是多少元?并写出总组装费用最少时的组装方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3的顶点为M(2,﹣1),交x轴于点A、B两点,交y轴于点C,其中点B的坐标为(3,0).
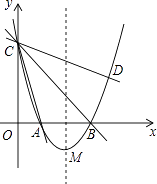
(1)求抛物线的解析式;
(2)设经过点C的直线与该抛物线的另一个点为D,且直线CD和直线CA关于直线CB对称,求直线CD的解析式;
(3)在该抛物线的对称轴上存在点P,满足PM2+PB2+PC2=35,求点P的坐标;并直接写出此时直线OP与该抛物线交点的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】作图与计算
(1)已知:
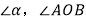 .
.求作:在图2中,以OA为一边,在∠AOB的内部作.∠AOC=
 (要求:直尺和圆规作图,不写作法,保留图痕迹.)
(要求:直尺和圆规作图,不写作法,保留图痕迹.)
(2)过点O分别引射线OA、OB、OC,且∠AOB=65°,∠BOC=30°,求∠AOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,两个大小不同的球在水平面上靠在一起,组成如图所示的几何体,则该几何体的左视图是( )

A.两个内切的圆
B.两个外切的圆
C.两个相交的圆
D.两个外离的圆
相关试题

