【题目】某公司决定利用仅有的349个甲种部件和295个乙种部件组装A、B两种型号的简易板房共50套捐赠给灾区.已知组装一套A型号简易板房需要甲种部件8个和乙种部件4个,组装一套B型号简易板房需要甲种部件5个和乙种部件9个.
(1)该公司组装A、B两种型号的简易板房时,共有多少种组装方案?
(2)若组装A、B两种型号的简易板房所需费用分别为每套200元和180元,问最少总组装费用是多少元?并写出总组装费用最少时的组装方案.
参考答案:
【答案】
(1)
解:设组装A型号简易板房x套,则组装B型号简易板房(50﹣x)套,
根据题意得出:
![]() ,
,
解得:31≤x≤33,
故该公司组装A、B两种型号的简易板房时,共有3种组装方案:
组装A型号简易板房31套,则组装B型号简易板房19套,
组装A型号简易板房32套,则组装B型号简易板房18套,
组装A型号简易板房33套,则组装B型号简易板房17套;
(2)
解:设总组装费用为W,
则W=200x+180(50﹣x)=20x+9000,
∵20>0,
∴W随x的增大而增大,
当x=31时,W最小=20×31+9000=9620(元).
此时x=31,50﹣31=19,
答:最少总组装费用是9620元,总组装费用最少时的组装方案为:组装A型号简易板房31套,则组装B型号简易板房19套.
【解析】(1)根据题中已知条件列出不等式组,解不等式租得出整数即可解得有3种组装方案;(2)根据组装方案的费用W关于x 的方程,解得当x=31时,组装费用W最小为9620元.
【考点精析】关于本题考查的一元一次不等式组的应用,需要了解1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
分数段
频数
频率
60≤x<70
40
0.40
70≤x<80
35
b
80≤x<90
a
0.15
90≤x<100
10
0.10
频率分布统计表
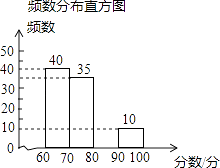
请根据上述信息,解答下列问题:
(1)分别求出a、b的值;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G.
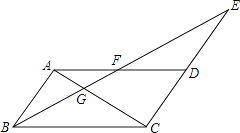
(1)求证:AF=DF;
(2)若BC=2AB,DE=1,∠ABC=60°,求FG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某苹果生产基地,用30名工人进行采摘或加工苹果 ,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售;另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4 000元;加工成罐头出售每吨获利10 000元.采摘的工人每人可采摘苹果0.4吨;加工罐头的工人每人可加工0.3吨.设有x名工人进行苹果采摘,全部售出后,总利润为y元.
(1)求y与x的函数关系式;
(2)如何分配工人才能获利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.
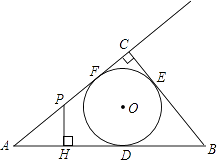
(1)直接写出线段AC、AD及⊙O半径的长;
(2)设PH=x,PC=y,求y关于x的函数关系式;
(3)当PH与⊙O相切时,求相应的y值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3的顶点为M(2,﹣1),交x轴于点A、B两点,交y轴于点C,其中点B的坐标为(3,0).
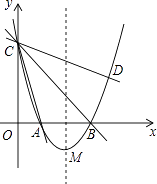
(1)求抛物线的解析式;
(2)设经过点C的直线与该抛物线的另一个点为D,且直线CD和直线CA关于直线CB对称,求直线CD的解析式;
(3)在该抛物线的对称轴上存在点P,满足PM2+PB2+PC2=35,求点P的坐标;并直接写出此时直线OP与该抛物线交点的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】作图与计算
(1)已知:
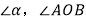 .
.求作:在图2中,以OA为一边,在∠AOB的内部作.∠AOC=
 (要求:直尺和圆规作图,不写作法,保留图痕迹.)
(要求:直尺和圆规作图,不写作法,保留图痕迹.)
(2)过点O分别引射线OA、OB、OC,且∠AOB=65°,∠BOC=30°,求∠AOC的度数.
相关试题

