【题目】如图,AC⊥BC于C,CD⊥AB于D,点E在AC上,EF⊥AB于F,且∠1=∠2.
(1)试判断CD与EF是否平行并说明理由.
(2)试判断DG与BC是否垂直并说明理由.

参考答案:
【答案】(1)CD∥EF;(2)DG⊥BC.
【解析】
(1)根据平行线的判定推出即可;
(2)根据平行线的性质得出∠1=∠ACD,求出∠2=∠ACD,根据平行线的判定得出DG∥AC,即可求出答案.
解:(1)CD∥EF,
理由是:∵CD⊥AB,EF⊥AB,
∴∠EFA=∠CDA=90°,
∴CD∥EF;
(2)DG⊥BC,
理由是:∵EF∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠2=∠ACD,
∴DG∥AC,
∴∠DGB=∠ACB,
∵AC⊥BC,
∴∠ACB=90°,
∴∠DGB=90°,
∴DG⊥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=41,AC=15,高AH=9,则△ABC的面积是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国宋朝数学家杨辉在他的著作《详解九章算术》中提出下表,此表揭示了(n为非负整数)展开式的各项系数的规律,例如:
(a+b)0=1,它只有一项,系数为1;
(a+b)1=a+b,它有两项,系数分别为1,1;
(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;
(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;…
根据以上规律,(a+b)6展开式共有______项,各项系数的和等于______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.
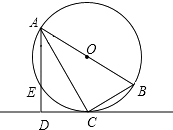
(1)求证:CD为⊙O的切线;
(2)若⊙O的直径为8cm,CD=2 cm,求弦AE的长.
cm,求弦AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算并观察下列各式:
第1个:(a﹣b)(a+b)=______;
第2个:(a﹣b)(a2+ab+b2)=______;
第3个:(a﹣b)(a3+a2b+ab2+b3)=_______;
……
这些等式反映出多项式乘法的某种运算规律.
(2)猜想:若n为大于1的正整数,则(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=________;
(3)利用(2)的猜想计算:2n﹣1+2n﹣2+2n﹣3+……+23+22+1=______.
(4)拓广与应用:3n﹣1+3n﹣2+3n﹣3+……+33+32+1=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD,解决下列问题:
(1)如图①,BP、DP分别平分∠ABE、∠CDE,若∠E=100°,求∠P的度数.
(2)如图②,若∠ABP=
 ∠ABE,∠CDP=
∠ABE,∠CDP= ∠CDE,试写出∠P与∠E的数量关系并说明理由.
∠CDE,试写出∠P与∠E的数量关系并说明理由.(3)如图③,若∠ABP=
 ∠ABE,∠CDP=
∠ABE,∠CDP= ∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).
∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).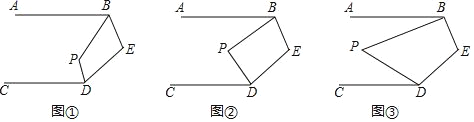
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.如果一条直线与果圆只有一个交点,则这条直线叫做果圆的切线.已知A、B、C、D四点为果圆与坐标轴的交点,E为半圆的圆心,抛物线的解析式为y=x2﹣2x﹣3,AC为半圆的直径.

(1)分别求出A、B、C、D四点的坐标;
(2)求经过点D的果圆的切线DF的解析式;
(3)若经过点B的果圆的切线与x轴交于点M,求△OBM的面积.
相关试题

