【题目】如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.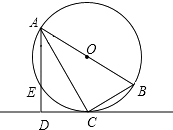
(1)求证:CD为⊙O的切线;
(2)若⊙O的直径为8cm,CD=2 ![]() cm,求弦AE的长.
cm,求弦AE的长.
参考答案:
【答案】
(1)证明:连接OC,如图所示:
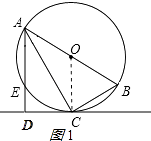
∵OA=OC,
∴∠OAC=∠0CA,
∵AC平分∠BAD,
∴∠OAC=∠CAD,
∴∠CAD=∠ACO,
∴OC∥AD,
∵CD⊥AD,
∴CD⊥OC,
∴CD为⊙O的切线;
(2)解:作OF⊥AE于F,如图2所示:
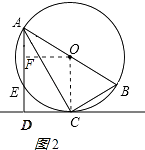
则AF= ![]() AE,四边形OFDC是矩形,
AE,四边形OFDC是矩形,
∴OF=CD=2 ![]() cm,
cm,
∵OA= ![]() AB=4cm,
AB=4cm,
∴AF= ![]() =
= ![]() =2,
=2,
∴AE=2AF=4.
【解析】(1)连接OC,根据等边对等角,角平分线的定义及等量代换得出∠CAD=∠ACO,从而根据内错角相等两直线平行得出OC∥AD,然后根据平行线的性质得出CD⊥OC,即CD为⊙O的切线;
(2)作OF⊥AE于F,根据垂径定理得出得出AF=![]() AE,根据三个角是直角得四边形是矩形得出四边形OFDC是矩形,根据矩形的对边相等得出OF=CD,然后利用勾股定理得出AF的长,从而得出AE的长。
AE,根据三个角是直角得四边形是矩形得出四边形OFDC是矩形,根据矩形的对边相等得出OF=CD,然后利用勾股定理得出AF的长,从而得出AE的长。
【考点精析】通过灵活运用平行线的判定与性质和垂径定理,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张师傅准备用长为8cm的铜丝剪成两段,以围成两个正方形的线圈,设剪成的两段铜丝中的一段的长为xcm,围成的两个正方形的面积之和为Scm2 .
(1)求S与x的函数关系式,并写出自变量的取值范围;
(2)当x取何值时,S取得最小值,并求出这个最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=41,AC=15,高AH=9,则△ABC的面积是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国宋朝数学家杨辉在他的著作《详解九章算术》中提出下表,此表揭示了(n为非负整数)展开式的各项系数的规律,例如:
(a+b)0=1,它只有一项,系数为1;
(a+b)1=a+b,它有两项,系数分别为1,1;
(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;
(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;…
根据以上规律,(a+b)6展开式共有______项,各项系数的和等于______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC⊥BC于C,CD⊥AB于D,点E在AC上,EF⊥AB于F,且∠1=∠2.
(1)试判断CD与EF是否平行并说明理由.
(2)试判断DG与BC是否垂直并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算并观察下列各式:
第1个:(a﹣b)(a+b)=______;
第2个:(a﹣b)(a2+ab+b2)=______;
第3个:(a﹣b)(a3+a2b+ab2+b3)=_______;
……
这些等式反映出多项式乘法的某种运算规律.
(2)猜想:若n为大于1的正整数,则(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=________;
(3)利用(2)的猜想计算:2n﹣1+2n﹣2+2n﹣3+……+23+22+1=______.
(4)拓广与应用:3n﹣1+3n﹣2+3n﹣3+……+33+32+1=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD,解决下列问题:
(1)如图①,BP、DP分别平分∠ABE、∠CDE,若∠E=100°,求∠P的度数.
(2)如图②,若∠ABP=
 ∠ABE,∠CDP=
∠ABE,∠CDP= ∠CDE,试写出∠P与∠E的数量关系并说明理由.
∠CDE,试写出∠P与∠E的数量关系并说明理由.(3)如图③,若∠ABP=
 ∠ABE,∠CDP=
∠ABE,∠CDP= ∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).
∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).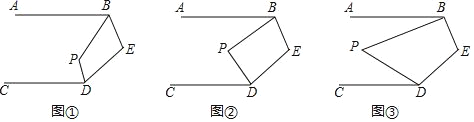
相关试题

