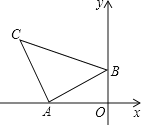
【题目】如图,△ABC是等腰直角三角形,∠BAC=90°,其中A(-2,0),B(0,1),则直线BC的函数表达式为______.
参考答案:
【答案】y=-![]() x+1
x+1
【解析】
先确定出OA=2,OB=1,再证明△AOB≌△CDA,得出AD=1,CD=2,求出C点坐标,然后利用待定系数法求出直线BC的函数表达式.
解:如图,∵A(-2,0),B(0,1),
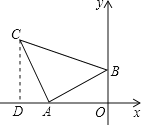
∴OA=2,OB=1.
过点C作CD⊥x轴于D,
∴∠CAD+∠ACD=90°,
∵∠BAC=90°,
∴∠CAD+∠OAB=90°,
∴∠OAB=∠ACD.
在△AOB和△CDA中,
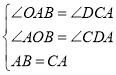 ,
,
∴△AOB≌△CDA,
∴AD=BO=1,CD=AO=2,
∴OD=OA+AD=3,
∴C(-3,2).
设直线BC的函数表达式为y=kx+b,
∵B(0,1),C(-3,2),
∴![]() ,
,
解得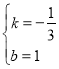 ,
,
∴直线BC的函数表达式为y=![]() x+1.
x+1.
故答案为y=![]() x+1.
x+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知 AD 与 BC 相交于 E ,1 2 3, BD CD, ADB 90, CH AB于 H , CH 交 AD 于 F 。
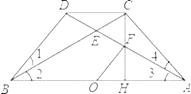
(1)求证: CD∥ AB ;
(2)求证: BDE ≌ ACE ;
(3)若O 为 AB 中点,求证:OF=
 BE 。
BE 。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图正方形ABCD中,点E、F分别在CD、BC边上,△AEF是等边三角形.以下结论:①EC=FC;②∠AED=75°;③AF=
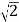 CE;④EF的垂直平分线是直线AC.正确结论个数有( )个.
CE;④EF的垂直平分线是直线AC.正确结论个数有( )个.
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在长方形ABCD中,AB=10 cm,BC=8 cm,点P从A出发,沿A、B、C、D路线运动,到D停止,点P的速度为每秒1 cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,△APD的面积S1(cm2)与y(秒)的函数关系图象:
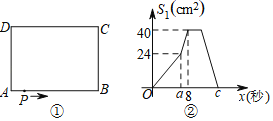
(1)根据图②中提供的信息,a= ,b= ,c= .
(2)点P出发后几秒,△APD的面积S1是长方形ABCD面积的四分之一?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为 2 的正方形 ABCD 中,点 P 、Q 分别是边 AB 、 BC 上的两个动点(与点 A 、B 、C 不重合)且始终保持 BP BQ, AQ QE ,QE 交正方形外角平分线CE 于点 E , AE 交CD 于点 F ,连结 PQ 。
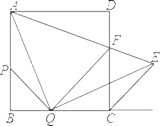
(1)求证: APQ ≌ QCE ;
(2)求QAE 的度数;
(3)设 BQ x ,当 x 为何值时, QF CE ,并求出此时AQF 的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形 ABCD 中,B 60 ,M 、N 分别为线段 AB 、BC 上的两点,且 BM CN , AN 、CM 相交于点 E 。
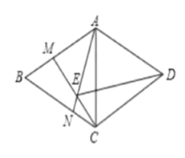
(1)证明: BCM ≌ CAN 。
(2)求AEM 的度数。
(3)证明: AE CE DE 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,

(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为3,AE=5,求∠DAE的正弦值.
相关试题

