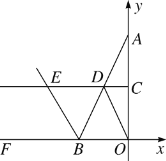
【题目】如图,在平面直角坐标系中,已知点A(0,6),B(b,0),且b<0,C,D分别是OA,AB的中点,△AOB的外角∠DBF的平分线BE与CD的延长线交于点E.
(1)求证:∠DAO=∠DOA;
(2)①若b=-8,求CE的长;
②若CE=![]() +1,则b=________;
+1,则b=________;
(3)是否存在这样的b值,使得四边形OBED为平行四边形?若存在,请求出此时四边形OBED对角线的交点坐标;若不存在,请说明理由.
参考答案:
【答案】(1)见解析;(2) ①9;②-2;(3)见解析.
【解析】(1)由C,D分别为AO,AB的中点,得到CD∥OB.又由OB⊥AO,得到CD垂直平分AO,由垂直平分线的性质即可得到结论.
(2)①由三角形中位线定理得到CD的长,由角平分线的定义和平行线的性质得到∠DEB=∠DBE,从而得到ED=BD=5,即可得到结论.
②由①得:EC=ED+DC=![]() AB+
AB+![]() BO,列方程求解即可得到结论.
BO,列方程求解即可得到结论.
(3)由四边形OBED是平行四边形,得OB=ED.由ED=BD=![]() AB,得到AB=-2b,于是有(-b)2+62=(-2b)2,解方程得到b的值,进而得到AB的长.设平行四边形OBED的对角线交点为M,作MH⊥OB于点H,则BM=
AB,得到AB=-2b,于是有(-b)2+62=(-2b)2,解方程得到b的值,进而得到AB的长.设平行四边形OBED的对角线交点为M,作MH⊥OB于点H,则BM=![]() BD=
BD=![]() AB.由OD=DB=OB,得到∠DBO=60°,∠BMH=30°,从而可得到BH,MH, OH,即可得到结论.
AB.由OD=DB=OB,得到∠DBO=60°,∠BMH=30°,从而可得到BH,MH, OH,即可得到结论.
(1)∵C,D分别为AO,AB的中点,∴CD∥OB.
又∵OB⊥AO,∴CD⊥AC,∴CD垂直平分AO,∴AD=OD,∴∠DAO=∠DOA.
(2)①∵b=-8,∴OB=8,∴CD=![]() OB=4.易得∠DEB=∠DBE,∴ED=BD=
OB=4.易得∠DEB=∠DBE,∴ED=BD=![]() AB=
AB=![]() =5,∴CE=CD+ED=4+5=9.
=5,∴CE=CD+ED=4+5=9.
②由①得:EC=ED+DC=![]() AB+
AB+![]() BO,∴
BO,∴![]() ,解得:b=-2.故答案为:-2.
,解得:b=-2.故答案为:-2.
(3)存在.理由如下:
如图,∵四边形OBED是平行四边形,∴OB=ED.
∵ED=BD=![]() AB,∴OB=
AB,∴OB=![]() AB.
AB.
∵OB=-b,∴AB=-2b,∴(-b)2+62=(-2b)2,解得:b=![]() ,∴AB=
,∴AB=![]() .设平行四边形OBED的对角线交点为M,作MH⊥OB于点H,则BM=
.设平行四边形OBED的对角线交点为M,作MH⊥OB于点H,则BM=![]() BD=
BD=![]() AB=
AB=![]() ×
×![]() =
=![]() .
.
∵OD=AD,∴OD=DB=OB,∴∠DBO=60°,∴∠BMH=30°,∴BH=![]() ,MH=
,MH=![]() ,∴OH=
,∴OH=![]() =
=![]() ,∴M(
,∴M(![]() ,
,![]() ).
).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,A、B在数轴上对应的数分别用
 、
、 表示,且
表示,且 .
.(1)数轴上点A表示的数是 ,点B表示的数是
(2)若一动点P从点A出发,以3个单位长度/秒速度由A向B运动;动点Q从原点O出发,以1个单位长度/秒速度向B运动,点P、Q同时出发,点Q运动到B点时两点同时停止.设点Q运动时间为t秒.
①若P从A到B运动,则P点表示的数为 ,Q点表示的数为 .用含
 的式子表示)
的式子表示)②当t为何值时,点P与点Q之间的距离为2个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板按如图方法摆放在一起,连接AC,则tan∠DAC值为( )

A.1
B.
C.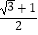
D.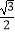
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(﹣3
 )﹣(﹣2
)﹣(﹣2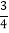 )﹣(﹣2
)﹣(﹣2 )﹣(+1.75)﹣(﹣1
)﹣(+1.75)﹣(﹣1 )
)(2)﹣4×(﹣2
 )﹣6×(﹣2
)﹣6×(﹣2 )+17×(﹣2
)+17×(﹣2 )﹣19
)﹣19 ÷
÷
(3)﹣12+
 ×[﹣22+(﹣3)2×(﹣2)+(﹣3)]÷(﹣
×[﹣22+(﹣3)2×(﹣2)+(﹣3)]÷(﹣ )2
)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC.M、N分别是AB、AC的中点,D、E为BC上的点,连接DN、EM.若AB=13cm,BC=10cm,DE=5cm,则图中阴影部分的面积为cm2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图象可能是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
相关试题

