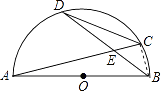
【题目】半圆O的直径AB=9,两弦AC、BD相交于点E,弦CD= ![]() ,且BD=7,则DE=
,且BD=7,则DE=
参考答案:
【答案】3 ![]()
【解析】根据圆周角定理得出的两组相等的对应角,易证得△AEB∽△DEC,根据CD、AB的长,即可求出两个三角形的相似比;设BE=x,则DE=7-x,然后根据相似比表示出AE、EC的长,连接BC,首先在Rt△BEC中,根据勾股定理求得BC的表达式,然后在Rt△ABC中,由勾股定理求得x的值,进而可求出DE的长.
∵∠D=∠A,∠DCA=∠ABD,
∴△AEB∽△DEC;
∴ ![]() ;
;
设BE=x,则DE=7-x,EC= ![]() x,AE=
x,AE= ![]() (7-x);
(7-x);
连接BC,则∠ACB=90°;
Rt△BCE中,BE=x,EC= ![]() x,则BC=
x,则BC= ![]() x;
x;
在Rt△ABC中,AC=AE+EC= ![]() -
- ![]() x,BC=
x,BC= ![]() x;
x;
由勾股定理,得:AB2=AC2+BC2,
即:92=( ![]() -
- ![]() x)2+(
x)2+( ![]() x)2,
x)2,
整理,得x2-14x+31=0,
解得:x1=7+3 ![]() (不合题意舍去),x2=7-3
(不合题意舍去),x2=7-3 ![]()
则DE=7-x=3![]() .
.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为a的正六边形内有两个三角形(数据如图),则
 =( )
=( ) 
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与⊙O相切于点A,AC,CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为
 ,CD=4,则弦AC的长为 .
,CD=4,则弦AC的长为 . 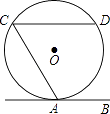
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某动物园的平面示意图,借助刻度尺、量角器,解决如下问题:
(1)猴园和鹿场分别位于水族馆的什么方向?
(2)与水族馆距离相同的地方有哪些场地?
(3)如果用(5,3)表示图上的水族馆的位置,那么猛兽区怎样表示?(7,5)表示什么区?
,

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
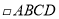 ,对角线AC、BD相交于点O.
,对角线AC、BD相交于点O.⑴若AB=BC,则
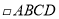 是_______.
是_______.⑵若AC=BD,则
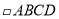 是_________.
是_________.⑶若∠BCD=90°,则
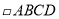 是_________.
是_________.⑷若OA=OB,且OA⊥OB,则
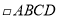 是_________.
是_________.⑸若AB=BC,且AC=BD,则
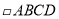 是_________.
是_________. -
科目: 来源: 题型:
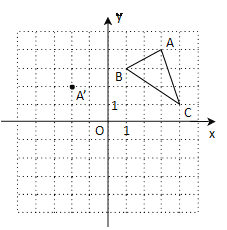
查看答案和解析>>【题目】在平面直角坐标系中,三角形ABC的三个顶点的位置如图所示,点A/的坐标是(—2,2),现将三角形ABC平移,使点A平移到A/,点B/、C/分别是B、C的对应点.
(1)请画出平移后的三角形A/B/C/,并直接写出点B/、C/的坐标;
(2)若三角形ABC内部一点P的坐标为(a,b),则点P的对应点P/的坐标是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)已知:sinα·cos60=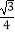 ,求锐角α;
,求锐角α;
(2)计算: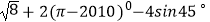 .
.
相关试题

