搜索
【题目】已知，如图，四边形ABCD中∠B=90°，AB=9，BC=12，AD=8，CD=17．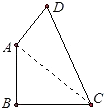 
试求：
（1）AC的长；
（2）四边形ABCD的面积．
参考答案：
【答案】
（1）解：∵∠B=90°，
∴AC= 
=15
（2）解：∵AC2+AD2=CD2，
∴∠CAD=90°，
∴四边形ABCD面积= 
=114
【解析】（1）已知∠B=90°，则△ABC是直角三角形，根据勾股定理解答即可；（2）根据△ACD的三边关系可判断出△ACD是直角三角形，再根据四边形ABCD面积=S△ABC+S△ACD计算．
【考点精析】认真审题，首先需要了解三角形的面积(三角形的面积=1/2×底×高)，还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若a2+b+5=0，则代数式3a2+3b+10=0的值为（ ）
A. 25 B. 5 C. -5 D. 0
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果∠α和∠β互补，且∠α＞∠β，则下列表示角的式子中：①90°﹣∠β；②∠α﹣90°；③
（∠α+∠β）；④ （∠α﹣∠β）．能表示∠β的余角的是（填写序号） -
科目： 来源： 题型：
查看答案和解析>>【题目】反比例函数
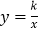在第一象限的图象如图所示，过点A（1，0）作x轴的垂线，交反比例函数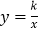的图象于点M，△AOM的面积为3．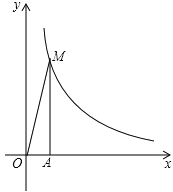
（1）求反比例函数的解析式；
（2）设点B的坐标为（t，0），其中t＞1．若以AB为一边的正方形有一个顶点在反比例函数
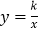的图象上，求t的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】老师在黑板上书写了一个正确的演算过程，随后用一张纸挡住了一个二次三项式，形式如下：
﹣3x=x2﹣5x+1
（1）求所挡的二次三项式；
（2）若x=﹣1，求所挡的二次三项式的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知x2-2x-8=0，则6x-3x2+18的值是（ ）
A. -6 B. 6 C. 42 D. -42
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了深化改革，某校积极开展校本课程建设，计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团，要求每位学生都自主选择其中一个社团．为此，随机调查了本校各年级部分学生选择社团的意向，并将调查结果绘制成如下统计图表（不完整）：
某校被调查学生选择社团意向统计表选择意向
所占百分比
文学鉴赏
a
科学实验
35%
音乐舞蹈
b
手工编织
10%
其他
c
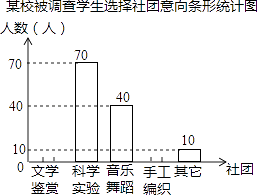
根据统计图表中的信息，解答下列问题：
（1）求本次调查的学生总人数及a，b，c的值；
（2）将条形统计图补充完整；
（3）若该校共有1200名学生，试估计全校选择“科学实验”社团的人数．
相关试题
