【题目】某林场计划购买甲、乙两种树苗共1000株,甲种树苗每株12元,乙种树苗每株15元.相关资料表明:甲、乙两种树苗的成活率分别为85%、90%.
(1)若购买这两种树苗共用去13200元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
参考答案:
【答案】(1)甲种树苗600株,乙种树苗400株;(2)400株
【解析】
(1)设购买甲种树苗![]() 株,乙种树苗
株,乙种树苗![]() 株.根据题意列出方程组求解可得;
株.根据题意列出方程组求解可得;
(2)设购买甲种树苗![]() 株,乙种树苗
株,乙种树苗![]() 株,根据题意列出不等式求解可得。
株,根据题意列出不等式求解可得。
解:(1)设购买甲种树苗![]() 株,乙种树苗
株,乙种树苗![]() 株.
株.
根据题意,得![]()
解,得![]()
答:购买甲种树苗600株,乙种树苗400株.
(2)设购买甲种树苗![]() 株,乙种树苗
株,乙种树苗![]() 株.
株.
由题意,得![]() .
.
解得![]() .
.
答:甲种树苗至多购买400株.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 的边长是4,
的边长是4, 的平分线交
的平分线交 于点
于点 ,若点
,若点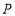 、
、 分别是
分别是 和
和 上的动点,则
上的动点,则 的最小值是__________.
的最小值是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学1000名学生参加了“环保知识竞赛”,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组
频数
频率
50≤x<60
8
0.16
60≤x<70
12
a
70≤x<80
■
0.5
80≤x<90
3
0.06
90≤x<90
b
c
合计
■
1
(1)写出
 ,
, ,
, 的值;
的值;(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
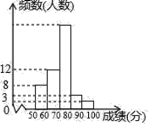
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
求证:四边形AFCE是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N.连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
相关试题

